Exercício Resolvido de Termodinâmica
publicidade
Calcular, em calorias, o trabalho necessário para vencer a pressão atmosférica de uma atmosfera durante a solidificação de 10 kg de água a 0° C. A massa específica do gelo é 0,917 g/cm3 a 0° C e a da água é 1 g/cm3. Adote o equivalente mecânico do calor como sendo 1 cal = 4,18 J.
Dados do problema:
- Massa de água: m = 10 kg;
- Pressão atmosférica: p = 1 atm;
- Massa específica do gelo: μg = 0,917 g/cm3;
- Massa específica da água: μa = 1 g/cm3;
- Equivalência entre caloria e joule: 1 cal = 4,18 J.
No início temos água a 0° C e no final temos gelo a 0° C, como não há mudança de temperatura podemos adotar que o recipiente não sofre mudança de volume durante o congelamento da água. Assim a área A da superfície do líquido será a mesma da superfície do gelo no final da transformação.
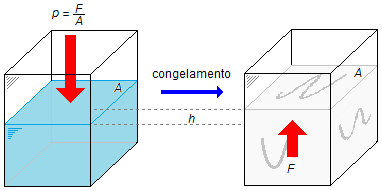
A superfície da água sofre uma pressão p da atmosfera devido à força (força peso) da coluna de ar sobre a superfície livre da água; Quando a água se congela ela se expande, como ela está contida pelas paredes laterais e inferior do recipiente ela só pode se expandir para cima, nesta expansão a superfície se desloca de uma altura h, para que este deslocamento ocorra a água deve exercer uma força F contra a pressão atmosférica.
Solução
Em primeiro lugar devemos converter as massas específicas, da água e do gelo, dadas em gramas por centímetro cúbico para quilogramas por metro cúbico e a pressão atmosférica dada em atmosferas para pascal, usadas no Sistema Internacional (S.I.)
\[
\begin{gather}
\mu_{g}=0,917\;\frac{\text{g}}{\text{cm}^{3}}.\frac{1\;\text{kg}}{1000\;\text{g}}.\frac{(100\;\text{cm})^{3}}{(1\;\text{m}\,)^{3}}=0,917\;\frac{\cancel{\text{g}}}{\cancel{\text{cm}^{3}}}.\frac{1\;\text{kg}}{1000\;\cancel{\text{g}}}.\frac{1000000\;\cancel{\text{cm}^{3}}}{1\;\text{m}^{3}}\text{=}\\
\text{=}0,917.1000\;\frac{\text{kg}}{\text{m}^{3}}=917\;\frac{\text{kg}}{\text{m}^{3}} \qquad\qquad\qquad\qquad\\[10pt]
\mu_{a}=1\;\frac{\text{g}}{\text{cm}^{3}}.\frac{1\;\text{kg}}{1000\;\text{g}}.\frac{(100\;\text{cm})^{3}}{(1\;\text{m})^{3}}=1\;\frac{\cancel{\text{g}}}{\cancel{\text{cm}^{3}}}.\frac{1\;\text{kg}}{1000\;\cancel{\text{g}}}.\frac{1000000\;\cancel{\text{cm}^{3}}}{1\;\text{m}^{3}}\text{=}\\
\text{=}1.1000\;\frac{\text{kg}}{\text{m}^{3}}=1000\;\frac{\text{kg}}{\text{m}^{3}} \qquad\qquad\qquad\qquad\quad\,\\[10pt]
p=1\;\text{atm}=1,01.10^{5}\;\text{Pa}
\end{gather}
\]
O trabalho da força realizada contra a pressão atmosférica é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{_{F}{\Large{\tau }}=Fd} \tag{I}
\end{gather}
\]
onde o deslocamento (d) é a altura que a superfície da água subiu enquanto se congelava, sendo
d=h.A pressão exercida pela força de expansão é dada por
\[ \bbox[#99CCFF,10px]
{p=\frac{F}{A}}
\]
\[
\begin{gather}
F=pA \tag{II}
\end{gather}
\]
substituindo a expressão (II) na expressão (I)
\[
\begin{gather}
_{F}{\Large{\tau }}=pAh \tag{III}
\end{gather}
\]
O termo Ah que aparece na expressão (III) representa a variação de volume ΔV entre o
volume final do gelo (Vg) e o volume inicial de água (Va) (Figura 2)
\[
\begin{gather}
Ah=\Delta V=V_{g}-V_{a} \tag{IV}
\end{gather}
\]
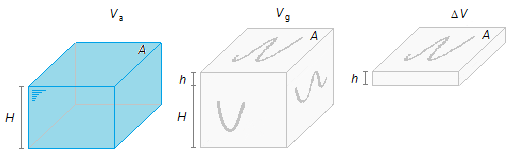
substituindo a expressão (IV) na expressão (III)
\[
\begin{gather}
_{F}{\Large{\tau}}=p\,\left(\,V_{g}-V_{a}\,\right) \tag{V}
\end{gather}
\]
A massa específica de um corpo é dada por
\[ \bbox[#99CCFF,10px]
{\mu =\frac{m}{V}}
\]
\[
V=\frac{m}{\mu}
\]
escrevendo esta expressão para os volumes de água e de gelo
\[
\begin{gather}
V_{a}=\frac{m}{\mu_{a}} \tag{VI-a}
\end{gather}
\]
\[
\begin{gather}
V_{g}=\frac{m}{\mu_{g}} \tag{VI-b}
\end{gather}
\]
substituindo as expressões (VI-a) e (VI-b) na expressão (V)
\[
_{F}{\Large{\tau }}=p\,\left(\,\frac{m}{\mu_{g}}-\frac{m}{\mu _{a}}\,\right)
\]
colocando a massa m em evidência
\[
_{F}{\Large{\tau }}=pm\;\left(\;\frac{1}{\mu_{g}}-\frac{1}{\mu_{a}}\;\right)
\]
substituindo os valores dados no problema
\[
\begin{gather}
_{F}{|Large{\tau}}=1,01.10^{5}.10.\;\left(\;\frac{1}{917}-\frac{1}{1000}\;\right)\\
_{F}{\Large{\tau}}=1,01.10^{4}.\;\left(\;0,0011-0,0010\;\right)\\
_{F}{\Large{\tau}}=10100.0,0001\\
_{F}{\Large{\tau}}=1,01\;\text{J}
\end{gather}
\]
Convertendo para calorias usamos a equivalência dada no problema fazendo uma “regra de três”
\[
\begin{gather}
\frac{1\;\text{cal}}{4,18\;\text{J}}=\frac{Q}{1,01\;\text{J}}\\
Q=\frac{1\;\text{cal}.(1,01\;\cancel{\text{J}})}{4,18\;\cancel{\text{J}}}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{Q=0,24\;\text{cal}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .