Exercício Resolvido de Termodinâmica
publicidade
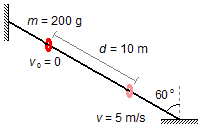
Um fio de arame está preso a uma parede numa de suas extremidades e ao solo na outra, é mantido tenso de modo a formar um ângulo de 60° com a vertical. Um anel de massa 200 g pode deslizar ao longo desse fio. A partir do repouso o anel se desloca por 10 m atingindo a velocidade de 5 m/s. Calcular o calor produzido pelo atrito entre o anel e o fio nesse deslocamento. Adote a aceleração da gravidade local igual a 10 m/s2 e o equivalente mecânico do calor como sendo 1 cal = 4,18 J.
Dados do problema:
- Massa do anel: m = 200 g;
- Velocidade inicial do anel: v0 = 0;
- Velocidade final do anel: v = 5 m/s;
- Distância percorrida pelo anel: d = 10 m;
- Ângulo de inclinação do fio: θ = 60°;
- Aceleração da gravidade local: g = 10 m/s2 ;
- Equivalência entre caloria e joule: 1 cal = 4,18 J.
Solução
Em primeiro lugar devemos converter a massa dada em gramas para quilogramas usadas no Sistema Internacional (S.I.)
\[
m=200\;\cancel{\text{g}}.\frac{1\;\text{kg}}{1000\cancel{\text{g}}}=0,2\;\text{kg}
\]
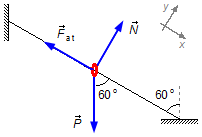
Adotamos um sistema de referência orientado na direção do arame com sentido descendente. No anel atuam as
seguintes forças (Figura 2):
- \( \vec{P} \): força peso;
- \( {\vec{F}}_{at} \): força de atrito;
- \( \vec{N} \): reação normal do arame sobre o anel.
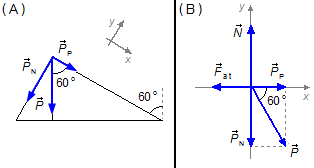
\[
\begin{gather}
P_{P}=P \cos 60° \tag{I-a}
\end{gather}
\]
\[
\begin{gather}
P_{N}=P \operatorname{sen}60° \tag{I-b}
\end{gather}
\]
O trabalho total
(\( \Large{\tau} \))
realizado será a soma dos trabalhos de todas as forças que atuam sobre o anel, trabalho da força de
atrito
(\( _{F_{at}}{\Large{\tau}} \)),
trabalho da componente paralela da força peso
(\( _{P_{P}}{\Large{\tau}} \)),
trabalho da componente normal da força peso
(\( _{P_{N}}{\large{\tau }} \))
e trabalho da reação normal
(\( _{N}{\Large{\tau}} \)).
\[
\begin{gather}
{\Large{\tau}}={_{F_{at}}}{\Large{\tau}}+{_{P_{P}}}{{\Large{\tau}}+{_{P_{N}}}{\Large{\tau}}+{_{N}}{\Large{\tau}}} \tag{II}
\end{gather}
\]
\[
\begin{gather}
\bbox[#99CCFF,10px]
{_{F}{\Large{\tau }}=Fd\cos \theta} \tag{III}
\end{gather}
\]
onde d é o deslocamento do corpo e θ é o ângulo entre a força e a direção de deslocamento.O trabalho da força de atrito é o que desejamos encontrar (\( _{F_{at}}{\Large{\tau }} \)).
- Aplicando a expressão (III) o trabalho da componente paralela da força peso é dado por
\[
\begin{gather}
_{{P}_{P}}{\Large{\tau }}=P_{P}d\cos \theta \tag{IV}
\end{gather}
\]
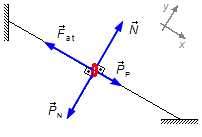
substituindo a expressão de (I-a) e o ângulo θ, entre a componente da força e a direção do deslocamento
(θ=0° - Figura 4 ), na expressão (IV),
\[
\begin{gather}
_{{P}_{P}}{\Large{\tau }}=P\,\cos 60°d\cos \theta \tag{V}
\end{gather}
\]
sendo a força peso dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{P=mg} \tag{VI}
\end{gather}
\]
substituindo a expressão (VI) na expressão (V)
\[
_{{P}_{P}}{\Large{\tau}}=mg\cos 60°d\cos 0°
\]
substituindo os valores dados e sendo
\( \cos 60°=\frac{1}{2} \)
e
\( \cos 0°=1 \)
\[
\begin{gather}
_{{P}_{P}}{\Large{\tau}}=0,2.10.\frac{1}{2}.10.1\\
_{{P}_{P}}{\Large{\tau}}=10\;\text{J} \tag{VII}
\end{gather}
\]
- O trabalho da componente normal da força peso é nulo
\[
\begin{gather}
_{{P}_{N}}{\Large{\tau }}=0 \tag{VIII}
\end{gather}
\]
pois a componente normal é perpendicular ( θ = 90° - Figura 4 ) ao deslocamento.
Observação: Fazendo o cálculo da componente normal da força peso
\[
\begin{gather}
_{{P}_{N}}{\Large{\tau}}=P_{N}d\cos \theta\\
_{{P}_{N}}{\Large{\tau}}=P_{N}d\cos 90°
\end{gather}
\]
sendo
\( \cos 90°=0 \)
\[
\begin{gather}
_{{P}_{N}}{\Large{\tau}}=0,2.10.\frac{1}{2}.10.0\\
_{{P}_{N}}{\Large{\tau}}=0
\end{gather}
\]
- O trabalho da reação normal também é nulo
\[
\begin{gather}
_{N}{\Large{\tau }}=0 \tag{IX}
\end{gather}
\]
pois a reação normal é perpendicular ( θ = 90° - Figura 4 ) ao deslocamento.
Observação: Fazendo o cálculo da reação normal
\[
\begin{gather}
_{N}{\Large{\tau }}=Nd\cos \theta\\
_{N}{\Large{\tau }}=Nd\cos 90°
\end{gather}
\]
sendo
\( \cos 90°=0 \),
não é preciso substituir os outros dados
\[
\begin{gather}
_{{P}_{N}}{\Large{\tau}}=\mathit{N.d.0}\\
_{{P}_{N}}{\Large{\tau}}=0
\end{gather}
\]
Substituindo as expressões (VII), (VIII) e (IX) na expressão (II)
\[
\begin{gather}
\tau =_{F_{at}}{\Large{\tau }}+10+0+0\\
\tau =_{F_{at}}{\Large{\tau }}+10 \tag{X}
\end{gather}
\]
Pelo Teorema da Energia Cinética o trabalho total realizado é igual a variação da energia cinética
entre dois pontos
\[
\begin{gather}
\tau =\frac{mv_{f}^{2}}{2}-\frac{mv_{i}^{2}}{2} \tag{XI}
\end{gather}
\]
substituindo os dados do problema
\[
\begin{gather}
\tau =\frac{0,2.5^{2}}{2}-\frac{0,2.0^{2}}{2}\\
\tau=\frac{0,2.25}{2}-\frac{0,2.0}{2}\\
\tau =0,1.25-0 \\
\tau=0,1.25 \\
\tau =2,5\;\text{J} \tag{XII}
\end{gather}
\]
substituindo o resultado (XII) na expressão (X)
\[
\begin{gather}
2,5=_{F_{at}}{\Large{\tau}}+10\\2,5-10=_{F_{at}}{\Large{\tau}}\\
_{F_{at}}{\Large{\tau}}=-7,5\;\text{J}
\end{gather}
\]
o sinal de negativo indica que é o trabalho de uma força resistiva.Convertendo para calorias usamos a equivalência dada no problema
\[
\begin{gather}
\frac{1\;\text{cal}}{4,18\;\text{J}}=\frac{Q}{-7,5\;\text{J}}\\
Q=\frac{1\;\text{cal}.(-7,5\;\text{J})}{4,18\;\text{J}}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{Q=-1,8\;\text{cal}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .