Um recipiente de vidro contém uma massa m0 de mercúrio a uma temperatura
t0 e uma massa m1, com m1 < m0,
quando aquecido a uma temperatura t1, dado o coeficiente de dilatação volumétrica do
mercúrio igual a γHg determinar o coeficiente de dilatação volumétrica do vidro.
Dados do problema:
- Massa inicial de mercúrio: m0;
- Massa final de mercúrio: m1;
- Temperatura inicial: t0;
- Temperatura final: t1;
- Coeficiente de dilatação volumétrica do mercúrio: γHg.
Esquema do problema:
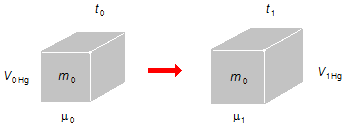
Inicialmente toda a massa m0 de mercúrio ocupa o volume V0R do
recipiente, após o aquecimento a massa m1 de mercúrio contida no volume
V1R do recipiente é menor, indicando que houve transbordamento de mercúrio
(Figura 1). O mercúrio se dilatou mais que o recipiente de vidro que o contém.
Solução:
A densidade de uma substância é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mu =\frac{m}{V}}
\end{gather}
\]
a densidade do mercúrio contido no recipiente nas duas situações é dada por
\[
\begin{gather}
\mu_0=\frac{m_0}{V_{0\small R}} \\[10pt]
\mu_1=\frac{m_1}{V_{1\small R}}
\end{gather}
\]
onde μ0 e μ1 são as densidades do mercúrio nas temperaturas
t0 e t1 respectivamente
\[
\begin{gather}
m_0=\mu_0V_{0\small R} \\[10pt]
m_1=\mu_1V_{1\small R}
\end{gather}
\]
dividindo a primeira equação pela segunda
\[
\begin{gather}
\frac{m_0}{m_1}=\frac{\mu_0V_{0\small R}}{\mu_1V_{1\small R}} \tag{I}
\end{gather}
\]
A dilatação volumétrica é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{V=V_0(1+\gamma \Delta t)}
\end{gather}
\]
Considerando apenas a dilatação do recipiente (Figura 2)
\[
\begin{gather}
V_{1\small R}=V_{0\small R}(1+\gamma_{\small V}\Delta t) \tag{II}
\end{gather}
\]
onde
\( \Delta t=t_1-t_0 \).
Considerando a dilatação de todo o volume de mercúrio (incluindo a parte que transbordou – Figura 3)
\[
\begin{gather}
V_{1\small{Hg}}=V_{0\small{Hg}}(1+\gamma_{\small{Hg}}\Delta t) \tag{III}
\end{gather}
\]
Usando novamente a equação da densidade, aplicado à toda massa de mercúrio nas duas situações
\[
\begin{gather}
\mu_0=\frac{m_0}{V_{0\small{Hg}}} \\[10pt]
\mu_1=\frac{m_0}{V_{1\small{Hg}}}
\end{gather}
\]
de onde obtemos
\[
\begin{gather}
V_{0\small{Hg}}=\frac{m_0}{\mu_0} \tag{IV-a} \\[10pt]
V_{1\small{Hg}}=\frac{m_0}{\mu_1} \tag{IV-b}
\end{gather}
\]
substituindo as equações (IV-a) e (IV-b) na equação (III)
\[
\begin{gather}
\frac{m_0}{\mu_1}=\frac{m_0}{\mu_0}(1+\gamma_{\small{Hg}}\Delta t) \\[5pt]
\mu_0=\frac{\mu_1m_0}{m_0}(1+\gamma_{\small{Hg}}\Delta t) \tag{V}
\end{gather}
\]
substituindo as equações (II) e (V) na equação (I)
\[
\begin{gather}
\frac{m_0}{m_1}=\frac{\dfrac{\cancel{\mu_1}\cancel{m_0}}{\cancel{m_0}}(1+\gamma_{\cancel{Hg}}\Delta t)\cancel{V_{0\small R}}}{\cancel{\mu_1}\cancel{V_{0\small R}}(1+\gamma_{V}\Delta t)} \\[5pt]
\frac{m_0}{m_1}=\frac{(1+\gamma_{\small{Hg}}\Delta t)}{(1+\gamma_{V}\Delta t)} \\[5pt]
m_0(1+\gamma_{V}\Delta t)=m_1(1+\gamma_{\small{Hg}}\Delta t) \\[5pt]
m_0+m_{0}\gamma_{V}\Delta t=m_1(1+\gamma_{\small{Hg}}\Delta t) \\[5pt]
m_0\gamma_{V}\Delta t=m_1(1+\gamma_{\small{Hg}}\Delta t)-m_0 \\[5pt]
\gamma_{V}=\frac{m_1(1+\gamma_{\small{Hg}}\Delta t)-m_0}{m_0\Delta t} \\[5pt]
\gamma_{V}=\frac{m_1(1+\gamma_{\small{Hg}}\Delta t)}{m_0\Delta t}-\frac{\cancel{m_0}}{\cancel{m_0}\Delta t} \\[5pt]
\gamma_{V}=\frac{m_1(1+\gamma_{\small{Hg}}\Delta t)}{m_0\Delta t}-\frac{1}{\Delta t}
\end{gather}
\]
colocando
\( \frac{1}{\Delta t} \)
em evidência no lado direito da igualdade
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\gamma_{V}=\left[\frac{m_1}{m_0}(1+\gamma_{\small{Hg}}\Delta t)-1\right]\frac{1}{\Delta t}}
\end{gather}
\]
