Exercício Resolvido de Lentes
publicidade
É dado um sistema ótico constituído por uma lente convergente L de distância focal f e de
centro óptico O, e um espelho plano E com a superfície refletora voltada para L e
inclinação de 45° em relação ao eixo da lente. A distância OE = d. Um objeto num ponto
P se desloca diante do espelho sobre a reta EA, normal ao eixo da lente. Pede-se:
a) Determinar a distância à lente da imagem P' conjugada pelo sistema espelho-lente ao ponto P, em função da distância x de P ao ponto E, fazendo a aplicação numérica para f = 50 cm, d = 30 cm e x = 70 cm;
b) Determinar para que valor de x os pontos P e P' são equidistantes de E.
a) Determinar a distância à lente da imagem P' conjugada pelo sistema espelho-lente ao ponto P, em função da distância x de P ao ponto E, fazendo a aplicação numérica para f = 50 cm, d = 30 cm e x = 70 cm;
b) Determinar para que valor de x os pontos P e P' são equidistantes de E.
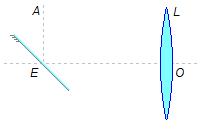
Construção da imagem:
No ponto P colocamos um objeto o de altura
\( \overline{PP_{1}} \).
Traçamos um segmento de reta r prolongando a direção do espelho. A partir de P traçamos
uma reta perpendicular (forma um ângulo de 90°) com r, e atrás do espelho, a mesma distância de
P, determinamos o ponto P2. A partir de P1 traçamos uma outra
reta e determinamos o ponto P3. O segmento
\( \overline{P_{2}P_{3}} \)
determina a imagem iE formada pelo espelho (Figura 1).
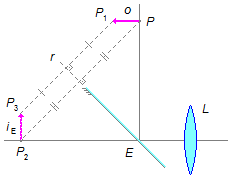
A distância do ponto P ao ponto E do espelho é x, como o ângulo entre o espelho e
o eixo da lente é de 45°, por simetria, a distância do ponto P2 (onde se forma a
imagem) ao ponto E também é x (Figura 2).
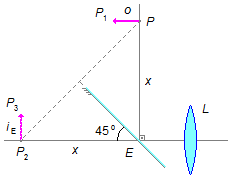
A imagem iE do espelho passa a ser o objeto oL para a lente. Usando a propriedade que todo raio que incide paralelamente ao eixo principal emerge numa direção que passa pelo foco imagem, assim este raio sai por F' (Figura 3).
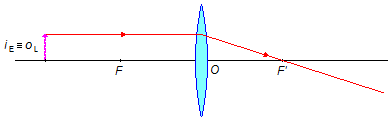
Tomando-se um segundo raio de luz com a propriedade que qualquer raio que passe pelo centro ótico da lente não sofre desvio ao atravessar a lente (Figura 4), do cruzamento dos dois raios temos a imagem formada pela lente iL.

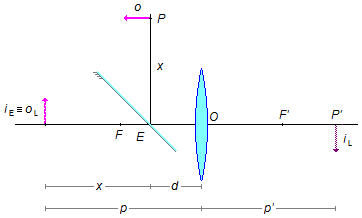
Esquema do problema:
Adotando-se a convenção de sinais onde do lado da luz incidente temos a abscissa positiva para o objeto real (p > 0) e negativa para a imagem virtual (p' < 0), do lado oposto temos a abscissa do objeto virtual negativa (p < 0) e positiva para a imagem real (p' > 0), Figura 5.

Solução
a) Da Figura 5 temos que a distância do objeto à lente (p) é a soma da distância do objeto ao espelho (x) com a distância do espelho à lente (d)
\[
\begin{gather}
p=x+d \tag{I}
\end{gather}
\]
Usando a Equação dos Pontos Conjugados
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\frac{1}{f}=\frac{1}{p}+\frac{1}{p'}} \tag{II}
\end{gather}
\]
substituindo a expressão (I) na expressão (II)
\[
\frac{1}{f}=\frac{1}{x+d}+\frac{1}{p'}
\]
a distância da imagem à lente (p'), será
\[
\frac{1}{p'}=\frac{1}{f}-\frac{1}{x+d}
\]
o fator comum entre f e x+d será f(x+d)
\[
\frac{1}{p'}=\frac{x+d-f}{f(x+d)}
\]
multiplicando em “cruz”
\[
f(x+d)=p'(x+d-f)
\]
\[ \bbox[#FFCCCC,10px]
{p'=\frac{f(x+d)}{(x+d-f)}}
\]
Fazendo a aplicação numérica dada no problema
\[
\begin{gather}
p'=\frac{50(70+30)}{(70+30-50)}\\
p'=\frac{50.100}{50}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{p'=100\;\text{cm}}
\]
b) A distância do ponto P ao espelho E é x, a distância do ponto P' ao espelho é p'+d, para que estas distâncias sejam iguais temos a condição
\[
\begin{gather}
x=p'+d \tag{III}
\end{gather}
\]
Observação: Não confundir os pontos P e P' onde estão colocados o objeto
(o) e a imagem da lente (iL), respectivamente, com p e p' as
distâncias da imagem do espelho e objeto para a lente
(\( i_{E}\equiv o_{L} \))
e a distância da imagem à lente (iL), respectivamente.
A distância do objeto à lente é dada por
\[
\begin{gather}
p=x+d \tag{IV}
\end{gather}
\]
Da expressão (III) temos o valor de p'
\[
\begin{gather}
p'=x-d \tag{V}
\end{gather}
\]
Substituindo os valores de (IV) e (V) na expressão (II)
\[
\frac{1}{f}=\frac{1}{x+d}+\frac{1}{x-d}
\]
substituindo os valore de f e d dados no problema
\[
\frac{1}{50}=\frac{1}{x+30}+\frac{1}{x-30}
\]
o fator comum entre x+30 e x−30 é
\( (x+30)(x-30)=x^{2}-900 \)
\[
\begin{gather}
\frac{1}{50}=\frac{x-30+x+30}{x^{2}-900}\\
\frac{1}{50}=\frac{2x}{x^{2}-900}
\end{gather}
\]
multiplicando em “cruz”
\[
\begin{gather}
x^{2}-900=50.2x\\
x^{2}-900=100x\\
x^{2}-100x-900=0
\end{gather}
\]
Esta é uma Equação do 2.º Grau onde a incógnita é o valor desejado x.
Solução da Equação do 2.º Grau \( x^{2}-100x-900=0 \)
\[
\begin{gather}
\Delta=b^{2}-4.a.c=(-100)^{2}-4.1.(-900)=10000+3600=13600\\[10pt]
x=\frac{-b\pm\sqrt{\;\Delta \;}}{2a}=\frac{-(-100)\pm\sqrt{13600\;}}{2.1}=\frac{100\pm 116,6}{2}
\end{gather}
\]
as duas raízes da equação serão
\[
\begin{gather}
x_{1}=108,3\\
\text{ou}\\
x_{2}=-8,3
\end{gather}
\]
Como x representa uma distância seu valor deve ser positivo (x>0), desprezando-se o valor negativo a resposta será x = 108,3 cm.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .