Exercício Resolvido de Lentes
publicidade
Um sistema óptico é formado por duas lentes delgadas justapostas. Uma das lentes é biconvexa de raios de curvatura 10 cm e 5 cm e índice de refração 1,7, a outra é convexo-côncava de raios de curvatura 10 cm e 20 cm e índice de refração 1,5. Calcular a altura da imagem de um objeto de 2 cm de altura a 10 cm de distância colocado normalmente ao eixo principal das lentes.
Dados do problema:
- Raios de curvatura (usando a convenção de que para a superfície convexa o raio é positivo e para a superfície côncava o raio é negativo), lente biconvexa.
- Superfície convexa: R1 = 10 cm;
- Superfície convexa: R2 = 5 cm;
- Índice de refração: nA = 1,7;
- Raios de curvatura lente convexo-côncava.
- Superfície côncava: R3 = −10 cm;
- Superfície convexa: R4 = 20 cm;
- Índice de refração: nB = 1,5;
- Altura do objeto: o = 2 cm;
- Distância do objeto à lente: p = 10 cm.
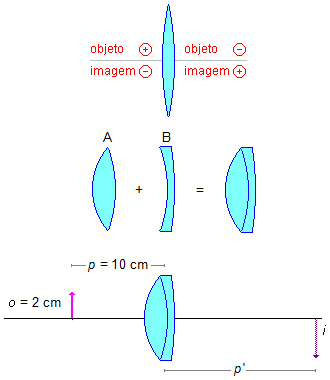
Adotando-se a convenção de sinais onde do lado da luz incidente temos a abscissa positiva para o objeto real (p > 0) e negativa para a imagem virtual (p' < 0), do lado oposto temos a abscissa do objeto virtual negativa (p < 0) e positiva para a imagem real (p' > 0), Figura 1.
Solução
Convertendo os raios de curvatura das lentes, o tamanho do objeto e a distância do objeto à lente, dadas em centímetros (cm), para metros (m)
\[
\begin{gather}
R_{1}=10\;\cancel{\text{cm}}.\frac{1\;\text{m}}{100\;\cancel{\text{cm}}}=0,1\;\text{m}\\[5pt]
R_{2}=5\;\cancel{\text{cm}}.\frac{1\;\text{m}}{100\;\cancel{\text{cm}}}=0,05\;\text{m}\\[5pt]
R_{3}=-10\;\cancel{\text{cm}}.\frac{1\;\text{m}}{100\;\cancel{\text{cm}}}=-0,1\;\text{m}\\[5pt]
R_{4}=20\;\cancel{\text{cm}}.\frac{1\;\text{m}}{100\;\cancel{\text{cm}}}=0,2\;\text{m}\\[5pt]
o=2\;\cancel{\text{cm}}.\frac{1\;\text{m}}{100\;\cancel{\text{cm}}}=0,02\;\text{m}\\[5pt]
p=10\;\cancel{\text{cm}}.\frac{1\;\text{m}}{100\;\cancel{\text{cm}}}=0,1\;\text{m}
\end{gather}
\]
Para uma associação de lentes a convergência do sistema será a soma das convergências de cada lente
\[
\begin{gather}
C=C_{A}+C_{B} \tag{I}
\end{gather}
\]
A distância focal é dada pela Fórmula dos Fabricantes de Lentes ou Equação de Halley
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\frac{1}{f}=\left(\frac{n_{2}}{n_{1}}-1\right)\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}\right)} \tag{II}
\end{gather}
\]
A convergência é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{C=\frac{1}{f}} \tag{III}
\end{gather}
\]
igualando as expressões (II) e (III) a convergência pode ser calculada por
\[
\begin{gather}
C=\left(\frac{n_{2}}{n_{1}}-1\right)\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}\right) \tag{IV}
\end{gather}
\]
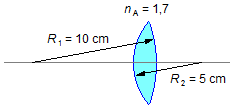
Para a primeira lente (biconvexa – Figura 2) o índice de refração da lente é
\( n_{2}=n_{A}=1,7 \),
o índice de refração do ar
\( n_{1}=1 \),
aplicando a expressão (IV)
\[
\begin{gather}
C_{A}=\left(\frac{n_{A}}{n_{1}}-1\right)\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}\right)\\[5pt]
C_{A}=\left(\frac{1,7}{1}-1\right)\left(\frac{1}{0,1}+\frac{1}{0,05}\right)\\[5pt]
C_{A}=0,7.(10+20)\\[5pt]
C_{A}=0,7.30\\[5pt]
C_{A}=21\;\text{di}
\end{gather}
\]
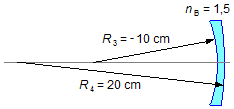
Para a segunda lente (convexo-côncava – Figura 3) o índice de refração da lente é \( n_{2}=n_{B}=1,5 \), pela expressão (IV)
\[
\begin{gather}
C_{B}=\left(\frac{n_{B}}{n_{1}}-1\right)\left(\frac{1}{R_{3}}+\frac{1}{R_{4}}\right)\\[5pt]
C_{B}=\left(\frac{1,5}{1}-1\right)\left(-{\frac{1}{0,1}}+\frac{1}{0,2}\right)\\[5pt]
C_{A}=0,5.(-10+5)\\[5pt]
C_{A}=0,5.(-5)\\[5pt]
C_{A}=-2,5\;\text{di}
\end{gather}
\]
Pela expressão (I) a convergência da associação será
\[
\begin{gather}
C=21+(-2,5)\\
C=18,5\;\text{di}
\end{gather}
\]
Usando a Equação dos Pontos Conjugados
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\frac{1}{f}=\frac{1}{p}+\frac{1}{p'}} \tag{V}
\end{gather}
\]
substituindo a expressão (III) na expressão (V)
\[
\begin{gather}
C=\frac{1}{p}+\frac{1}{p'} \tag{VI}
\end{gather}
\]
substituindo a convergência calculada acima e a distância do objeto à lente dada no problema
\[
\begin{gather}
18,5=\frac{1}{0,1}+\frac{1}{p'}\\18,5=10+\frac{1}{p'}\\
\frac{1}{p'}=18,5-10\\
\frac{1}{p'}=8,5\\
p'=\frac{1}{8,5}\\
p'=0,12\;\text{m}
\end{gather}
\]
Aplicando a Equação do Aumento Linear com os dados obtidos temos o tamanho da imagem
\[ \bbox[#99CCFF,10px]
{A=\frac{i}{o}=\frac{-{p'}}{p}}
\]
\[
\begin{gather}
\frac{i}{0,02}=\frac{-{0,12}}{0,1}\\
i=\frac{-{0,02.0,12}}{0,1}\\
i=\frac{-{0,0024}}{0,1}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{i=-0,024\;\text{m}=-2,4\;\text{cm}}
\]
Observação: O sinal de negativo da imagem indica que ela é invertida.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .