Exercício Resolvido de Espelhos Esféricos
publicidade
Diante de um espelho esférico côncavo cujo raio de curvatura mede 80 cm coloca-se um segmento retilíneo luminoso AB. Determinar a posição e a dimensão da imagem de AB. São dados AA1 = 2 cm, BB1 = 4 cm, A1V = 100 cm e B1V= 120 cm.
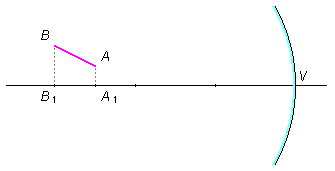
Dados do problema:
- Raio de curvatura do espelho: R = 80 cm;
- Altura do ponto A: AA1 = yA = 2 cm;
- Altura do ponto B: BB1 = yB = 4 cm;
- Distância do ponto A1 ao vértice do espelho: A1V = pA = 100 cm;
- Distância do ponto B1 ao vértice do espelho: B1V = pB = 120 cm.
Adota-se um Referencial de Gauss, sendo positiva a direção horizontal de onde vem o raio de luz (a esquerda, onde está o objeto) e para cima na direção vertical (Figura 1).
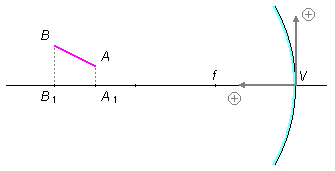
Usando a propriedade dos espelhos esféricos que diz que todo raio de luz que incide paralelamente ao eixo principal é refletido passando pelo foco principal do espelho (Figura 2).
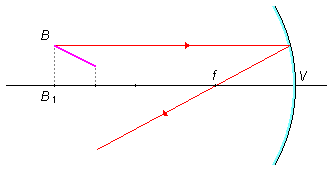
Tomando-se um segundo raio com a propriedade de que todo raio de luz que incide no vértice do espelho reflete-se de forma simétrica ao eixo principal (Figura 3). No cruzamento dos raios refletidos determina-se o ponto B’ de abscissa B’1.

De forma análoga um raio de luz que parte do ponto A é refletido pelo foco (Figura 4).
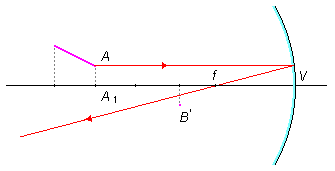
E um raio que incide no vértice é refletido simetricamente (Figura 5), e no ponto de cruzamento fica determinado o ponto A’ de abscissa A’1.
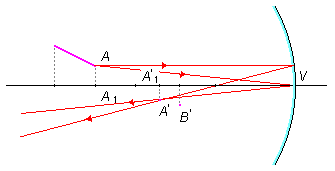
Os pontos A’ e B’ vão determinar a imagem do objeto AB.
Esquema do problema:
Observando a Figura 6 temos os seguintes elementos no problema
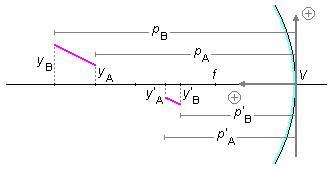
Solução
A distância do foco ao vértice será dada por
\[ \bbox[#99CCFF,10px]
{f=\frac{R}{2}}
\]
\[
\begin{gather}
f=\frac{80}{2}\\
f=40\;\text{cm}
\end{gather}
\]
Para o cálculo da distância da imagem ao espelho utilizamos a Equação dos Pontos Conjugados
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\frac{1}{f}=\frac{1}{p}+\frac{1}{p'}} \tag{I}
\end{gather}
\]
E para o cálculo do tamanho da imagem usamos a Equação do Aumento Linear Transversal
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\frac{i}{o}=-{\frac{p'}{p}}} \tag{II}
\end{gather}
\]
Aplicando a expressão (I) a distância p’A do ponto A será
\[
\begin{gather}
\frac{1}{f}=\frac{1}{p_{A}}+\frac{1}{p'_{A}}\\
\frac{1}{p'_{A}}=\frac{1}{f}-\frac{1}{p_{A}}\\
\frac{1}{p'_{A}}=\frac{1}{40}-\frac{1}{100}
\end{gather}
\]
o Mínimo Múltiplo Comum (M.M.C.) entre 40 e 100 é 200
\[
\begin{gather}
\frac{1}{p'_{A}}=\frac{5-2}{200}\\
\frac{1}{p'_{A}}=\frac{3}{200}\\
p'_{A}=\frac{200}{3} \tag{III}\\
p'_{A}=66,7\;\text{cm}
\end{gather}
\]
Aplicando a expressão (II) a altura y’A do ponto A será
\[
\frac{y'_{A}}{y_{A}}=-{\frac{p'_{A}}{p_{A}}}
\]
substituindo os dados fornecidos, e para o valor de p’A usamos a forma de (III) para
facilitar os cálculos
\[
\begin{gather}
\frac{y'_{A}}{2}=-{\frac{\dfrac{200}{3}}{100}}\\
y'_{A}=-2.\frac{200}{3}.\frac{1}{100}\\
y'_{A}=-{\frac{4}{3}} \tag{IV}\\
y'_{A}=-1,33\;\text{cm}
\end{gather}
\]
Aplicando a expressão (I) a distância p’B do ponto B será
\[
\begin{gather}
\frac{1}{f}=\frac{1}{p_{B}}+\frac{1}{p'_{B}}\\
\frac{1}{p'_{B}}=\frac{1}{f}-\frac{1}{p_{B}}\\
\frac{1}{p'_{B}}=\frac{1}{40}-\frac{1}{120}
\end{gather}
\]
o Mínimo Múltiplo Comum (M.M.C.) entre 40 e 120 é 120
\[
\begin{gather}
\frac{1}{p'_{B}}=\frac{3-1}{120}\\
\frac{1}{p'_{B}}=\frac{2}{120}\\
p'_{B}=\frac{120}{2}\\
p'_{B}=60\;\text{cm} \tag{V}
\end{gather}
\]
Aplicando a expressão (II) a altura y’B do ponto B será
\[
\begin{gather}
\frac{y'_{B}}{y_{B}}=-{\frac{p'_{B}}{p_{B}}}\\
\frac{y'_{B}}{4}=-{\frac{60}{120}}\\
y'_{B}=-4.\frac{1}{2}\\
y'_{B}=-2\;\text{cm} \tag{VI}
\end{gather}
\]
Para encontrarmos a dimensão (d) do objeto utilizamos as distâncias e tamanhos da imagem encontrados
em (III), (IV), (V) e (VI) representando esses valores no próprio Referencial de Gauss do problema
como mostrado na Figura 7.
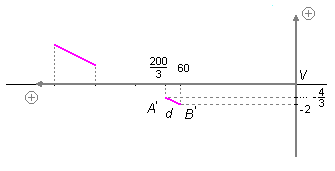
Para o cálculo da distância entre os pontos A’ e B’ aplicamos a Equação de Distância de Ponto a Ponto
\[ \bbox[#99CCFF,10px]
{d(a,b)=\sqrt{\left(x_{a}-x_{b}\right)^{2}+\left(y_{a}-y_{b}\right)^{2}\;}}
\]
\[
\begin{gather}
d(A',B')=\sqrt{\left(p'_{A}-p'_{B}\right)^{2}+\left(y'_{A}-y'_{B}\right)^{2}\;}\\
d(A',B')=\sqrt{\left(\frac{200}{3}-60\right)^{2}+\left(-{\frac{4}{3}}-(-2)\right)^{2}\;}\\
d(A',B')=\sqrt{\left(\frac{200-180}{3}\right)^{2}+\left(\frac{-4+6}{3}\right)^{2}\;}\\
d(A',B')=\sqrt{\left(\frac{20}{3}\right)^{2}+\left({\frac{2}{3}}\right)^{2}\;}\\
d(A',B')=\sqrt{\frac{400}{9}+\frac{4}{9}\;}\\
d(A',B')=\sqrt{\frac{404}{9}\;}\\
d(A',B')=\sqrt{44,9\;}\\
d(A',B')=6,7\;\text{cm}
\end{gather}
\]
A posição e dimensão da imagem serão
A’A’1 = 1,33 cm ;
B’B’1 = 2 cm;
A’1V = 66,7 cm;
B’1V = 60 cm;
A’B’ = 6,8 cm.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .