Exercício Resolvido de Dioptro
publicidade
Um hemisfério de raio R é feito de um material transparente de índice de refração igual a
\( \sqrt{2\;} \)
e sua superfície curva é espelhada. Um raio de luz incide perpendicularmente a face plana a uma distância
x do eixo do hemisfério. Determinar:
a) Qual a maior distância x para que o raio sofra apenas uma reflexão na face espelhada;
b) Se R = 5 cm quanto vale x?
a) Qual a maior distância x para que o raio sofra apenas uma reflexão na face espelhada;
b) Se R = 5 cm quanto vale x?
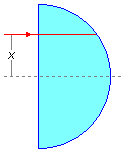
Dados do problema:
- Raio do hemisfério: R;
- Índice de refração do hemisfério: \( n=\sqrt{2\;} \);
- adotando que o sistema esteja imerso no ar, índice de refração do ar: nar = 1;
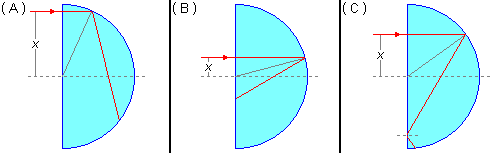
Se a distância x do raio ao eixo for muito grande o raio sofrerá mais de uma reflexão no interior (Figura 1-A), se x for muito pequeno o raio sofrerá apenas uma reflexão, mas este valor pode não ser o x máximo (Figura1-B) e podemos ter um x, tal que ocorra uma só reflexão, mas o ângulo de saída da face plana seja maior que o ângulo limite, então raio é refletido de volta para o interior (Figura 1-C).
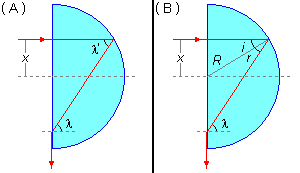
O ângulo limite λ e o ângulo de reflexão na face espelhada λ’ são iguais, pois são alternos
internos (Figura 2-A). O raio R do hemisfério é a normal no ponto de incidência do raio, então pela
lei da reflexão, os ângulos de incidência (i) e de reflexão (r) são iguais (Figura 2-B).
Solução
a) O ângulo limite é calculado por
\[ \bbox[#99CCFF,10px]
{\operatorname{sen}\lambda =\frac{n_{1}}{n_{2}}}
\]
onde n1 é o índice de refração do meio para onde o raio sai, no problema o ar, e
n2 é o índice de refração do meio de onde o raio está saindo, no problema o hemisfério.
\[
\operatorname{sen}\lambda =\frac{n_{ar}}{n}=\frac{1}{\sqrt{2\;}}
\]
multiplicando o numerador e o denominador por
\( \sqrt{2\;} \),
temos
\[
\operatorname{sen}\lambda=\frac{1}{\sqrt{2\;}}\frac{\sqrt{2\;}}{\sqrt{2\;}}=\frac{\sqrt{2\;}}{2}
\]
para encontrar o ângulo limite (λ) temos que achar o ângulo cujo arco seno é
\( \frac{\sqrt{2\;}}{2} \)
\[
\begin{gather}
\lambda =\operatorname{arc sen}\left(\frac{\sqrt{2\;}}{2}\right)\\
\lambda=45{}^{\circ}
\end{gather}
\]
Da Figura 2-B, podemos escrever
\[
\begin{gather}
\operatorname{sen}i=\frac{\text{cateto oposto}}{\text{hipotenusa}}=\frac{x}{R}\\
x=R\operatorname{sen}i \tag{I}
\end{gather}
\]
Observação: Lembrando da Trigonometria das propriedades de cosseno da soma dos ângulos e do cosseno
da diferença
\[
\begin{gather}
\cos(a+b)=\cos a\cos b-\operatorname{sen}a\operatorname{sen}b\\
\cos(a-b)=\cos a\cos b+\operatorname{sen}a\operatorname{sen}b
\end{gather}
\]
Sendo \( i+r=\lambda \), \( i-r=0 \) e \( i=r \)
\[
\begin{gather}
\cos(i+r)=\cos i\cos r-\operatorname{sen}i\operatorname{sen}r\\
\cos(i-r)=\cos i\cos r+\operatorname{sen}i\operatorname{sen}r\\
\cos \lambda =\cos i\cos i-\operatorname{sen}i\operatorname{sen}i\\
\cos 0°=\cos i\cos i+\operatorname{sen}i\operatorname{sen}i\\
\cos \lambda =\cos^{2}i-\operatorname{sen}^{2}i\\
\cos 0°=\cos^{2}i+\operatorname{sen}^{2}i
\end{gather}
\]
Como
\( \lambda =45° \),
temos
\( \cos \lambda =\cos 45°=\frac{\sqrt{2\;}}{2} \)
e
\( \cos 0°=1 \),
as expressões acima ficam
\[
\begin{gather}
\frac{\sqrt{2\;}}{2}=\cos ^{2}i-\operatorname{sen}^{2}i\tag{II}
\end{gather}
\]
\[
\begin{gather}
1=\cos ^{2}i+\operatorname{sen}^{2}i \tag{III}
\end{gather}
\]
subtraindo a expressão (II) da expressão (III)
\[
\begin{gather}
\frac{
\begin{matrix}
1=\cos^{2}i+\operatorname{sen}^{2}i \quad\; \\
\dfrac{\sqrt{2\;}}{2}=\cos^{2}i-\operatorname{sen}^{2}i \qquad \text{(-)}
\end{matrix}}
{1-\dfrac{\sqrt{2\;}}{2}=0+2\operatorname{sen}^{2}i \quad }\\[5pt]
2\operatorname{sen}^{2}i=1-\frac{\sqrt{2\;}}{2}\\[5pt]
\operatorname{sen}^{2}i=\frac{1}{2}-\frac{\sqrt{2\;}}{4}
\end{gather}
\]
colocando o fator
\( \frac{1}{4} \)
em evidência do lado direito da igualdade
\[
\begin{gather}
\operatorname{sen}^{2}i=\frac{1}{4}\left(2-\sqrt{2\;}\right)\\[5pt]
\operatorname{sen}i=\sqrt{\frac{1}{4}\left(2-\sqrt{2\;}\right)\;}\\[5pt]
\operatorname{sen}i=\frac{1}{2}\sqrt{2-\sqrt{2\;}} \tag{IV}
\end{gather}
\]
substituindo a expressão (IV) na expressão (I)
\[ \bbox[#FFCCCC,10px]
{x=\frac{R}{2}\sqrt{2-\sqrt{2\;}}}
\]
b) Substituindo o valor de R dado
\[
\begin{gather}
x=\frac{5}{2}\sqrt{2-\sqrt{2\;}}\\
x=1,9\;\text{cm}
\end{gather}
\]
A maior distância do eixo que um raio pode incidir para que haja uma só reflexão é
1,9 cm.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .