Exercício Resolvido de Fluidos

Um cone reto de altura H e massa específica μ flutua num líquido de massa específica μ _L, com o vértice para fora. Calcular a altura da parte imersa.

Dados do problema:

Altura do cone: H;
Massa específica do cone: μ;
Massa específica do líquido: μ_L.

Esquema do problema:

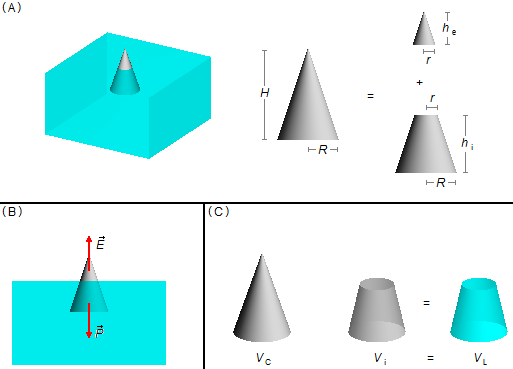
Seja R o raio da base do cone de altura H (Figura 1-A), este pode ser dividido em duas partes, um cone emerso, de altura h_e e raio r, e um tronco de cone imerso, de altura h_i e raio inferior R e raio superior r. A altura do cone será dada pela soma das alturas das duas partes

\[ \begin{gather} H=h_{e}+h_{i} \tag{I} \end{gather} \]

O volume do cone (V_C) é dado pela soma do cone emerso (V_e) com o volume do tronco de cone imerso (V_i)

\[ \begin{gather} V_{C}=V_{e}+V_{i} \tag{II} \end{gather} \]

Figura 1

As forças que atuam no cone são a força peso \( \vec{P} \) e a força de empuxo \( \vec{E} \), conforme a Figura 1-B. A força peso é devido à massa de todo cone de volume V_C, e a força de empuxo é devido à massa de líquido deslocado pelo tronco de cone imerso de volume V_i (Figura 1-C).

Solução

Adotando g para a aceleração local da gravidade o peso do cone é dado por

\[ \begin{gather} \bbox[#99CCFF,10px] {P=mg} \end{gather} \]

\[ \begin{gather} P_{C}=m_{C}g \tag{III} \end{gather} \]

a força de empuxo é dada por

\[ \begin{gather} \bbox[#99CCFF,10px] {E=m_{L}g} \tag{IV} \end{gather} \]

onde m_L é massa de líquido deslocada.
Para que o cone flutue devemos ter a condição

\[ \begin{gather} \sum_{i}F_{i}=0 \end{gather} \]

aplicando esta condição ao sistema (Figura 1-B)

\[ \begin{gather} E-P=0 \tag{V} \end{gather} \]

substituindo as expressões (III) e (IV) na expressão (V)

\[ \begin{gather} m_{L}g-m_{C}g=0\\[5pt] m_{L}\cancel{g}=m_{C}\cancel{g}\\[5pt] m_{L}=m_{C} \tag{VI} \end{gather} \]

A massa específica é dada por

\[ \begin{gather} \bbox[#99CCFF,10px] {\mu =\frac{m}{V}} \end{gather} \]

com o volume de líquido deslocado (V_L) é visto como um tronco de cone com o mesmo volume do tronco de cone imerso (V_i = V_L), aplicando esta expressão ao corpo e ao líquido

\[ \begin{gather} \mu =\frac{m_{C}}{V_{C}}\\[5pt] m_{C}=\mu V_{C} \tag{VII} \end{gather} \]

\[ \begin{gather} \mu _{L}=\frac{m_{L}}{V_{i}}\\[5pt] m_{L}=\mu_{L}V_{i} \tag{VIII} \end{gather} \]

substituindo as expressões (VII) e (VIII) na expressão (VI)

\[ \begin{gather} \mu_{L}V_{i}=\mu V_{C} \tag{IX} \end{gather} \]

Da expressão (II) podemos escrever o volume da parte imersa em termos dos volumes do cone e da parte emersa

\[ \begin{gather} V_{i}=V_{C}-V_{e} \tag{X} \end{gather} \]

substituindo a expressão (X) na expressão (IX)

\[ \begin{gather} \mu_{L}\left(V_{C}-V_{e}\right)=\mu V_{C}\\[5pt] \mu_{L}V_{C}-\mu_{L}V_{e}=\mu V_{C} \tag{XI} \end{gather} \]

O volume de um cone é dado por

\[ \begin{gather} \bbox[#99CCFF,10px] {V=\frac{1}{3}\pi r^{2}h} \end{gather} \]

Escrevendo o volume do cone total e o volume da parte emersa

\[ \begin{gather} V_{C}=\frac{1}{3}\pi R^{2}H \tag{XII-a} \end{gather} \]

\[ \begin{gather} V_{e}=\frac{1}{3}\pi r^{2}h_{e} \tag{XII-b} \end{gather} \]

substituindo as expressões (XII-a) e (XII-b) na expressão (XI)

\[ \begin{gather} \mu_{L}\cancel{\frac{1}{3}\pi} R^{2}H-\mu_{L}\cancel{\frac{1}{3}\pi} r^{2}h_{e}=\mu\cancel{\frac{1}{3}\pi} R^{2}H\\[5pt] \mu_{L}R^{2}H-\mu_{L}r^{2}h_{e}=\mu R^{2}H\\[5pt] \mu_{L}R^{2}H-\mu R^{2}H=\mu_{L}r^{2}h_{e}\\[5pt] R^{2}H\left(\mu_{L}-\mu \right)=\mu_{L}r^{2}h_{e}\\[5pt] h_{e}=\frac{R^{2}H\left(\mu_{L}-\mu \right)}{\mu_{L}r^{2}}\\[5pt] h_{e}=\frac{R^{2}H}{r^{2}}\left(\frac{\mu_{L}-\mu}{\mu_{L}}\right)\\[5pt] h_{e}=H\frac{R^{2}}{r^{2}}\left(\frac{\mu_{L}}{\mu_{L}}-\frac{\mu }{\mu_{L}}\right)\\[5pt] h_{e}=H\left(\frac{R}{r}\right)^{2}\left(1-\frac{\mu}{\mu_{L}}\right) \tag{XIII} \end{gather} \]

A razão entre os raios do cone e da parte emersa \( \left(\frac{R}{r}\right) \) pode ser obtido observando-se que uma seção transversal que passa pelo meio cone é um triângulo, metade desse triângulo forma um triângulo retângulo (Figura 2). Aplicando a Semelhança de Triângulos

\[ \begin{gather} \frac{H}{R}=\frac{h_{e}}{r}\\[5pt] \frac{R}{r}=\frac{H}{h_{e}} \tag{XIV} \end{gather} \]

Figura 2

substituindo a expressão (XIV) na expressão (XIII)

\[ \begin{gather} h_{e}=H\left(\frac{H}{h_{e}}\right)^{2}\left(1-\frac{\mu}{\mu_{L}}\right) \tag{XV} \end{gather} \]

da expressão (I) temos a altura do cone emerso

\[ \begin{gather} h_{e}=H-h_{i} \tag{XVI} \end{gather} \]

substituindo a expressão (XVI) na expressão (XV)

\[ \begin{gather} H-h_{i}=H\left(\frac{H}{H-h_{i}}\right)^{2}\left(1-\frac{\mu}{\mu_{L}}\right)\\[5pt] H-h_{i}=HH^{2}\frac{1}{{\left(H-h_{i}\right)}^{2}}\left(1-\frac{\mu}{\mu_{L}}\right)\\[5pt] \left(H-h_{i}\right)\left(H-h_{i}\right)^{2}=H^{3}\left(1-\frac{\mu}{\mu_{L}}\right)\\[5pt] \left(H-h_{i}\right)^{3}=H^{3}\left(1-\frac{\mu}{\mu_{L}}\right)\\[5pt] H-h_{i}=\sqrt[{3\;}]{H^{3}\left(1-\frac{\mu }{\mu_{L}}\right)\;}\\[5pt] H-h_{i}=H\sqrt[{3\;}]{1-\frac{\mu }{\mu_{L}}\;}\\[5pt] h_{i}=H-H\sqrt[{3\;}]{1-\frac{\mu }{\mu_{L}}\;} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {h_{i}=H\left(1-\sqrt[{3\;}]{1-\frac{\mu }{\mu_{L}}\;}\right)} \end{gather} \]

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .