Exercício Resolvido de Fluidos
publicidade
Um corpo de massa m e densidade dC é abandonado, em repouso, sobre a superfície livre de uma camada de líquido de altura h e densidade dL. Sendo dL < dC e a aceleração da gravidade igual a g, determinar:
a) O intervalo de tempo que o corpo leva para chegar ao fundo;
b) A energia cinética do corpo ao atingir o fundo.
Dados do problema:
- Massa do corpo: m;
- Densidade do corpo: dC;
- Velocidade inicial do corpo: v0 = 0;
- Espessura da camada de líquido: S = h;
- Densidade do líquido: dL;
- Aceleração da gravidade: g.
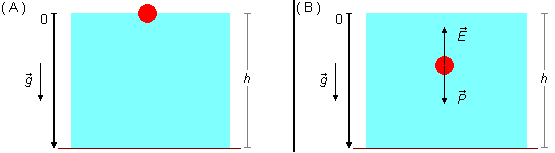
Adotamos um sistema de referência com origem na superfície do líquido e orientado para baixo (Figura 1-A). Inicialmente o corpo está em repouso (v0 = 0) como a densidade do corpo é maior que a do líquido (dC > dL) ele começa a afundar sob a ação da força peso \( \vec P \), e da resistência da força de empuxo \( \vec E \) devido ao líquido deslocado (Figura 1-B).
Solução
a) Aplicando a 2.ª Lei de Newton às forças da Figura 1-B
\[ \bbox[#99CCFF,10px]
{\vec{F}=m\vec{a}}
\]
\[
\begin{gather}
P-E=ma \tag{I}
\end{gather}
\]
onde a força peso é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{P=mg} \tag{II}
\end{gather}
\]
onde m é a massa do corpo, e a força de empuxo é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{E=m_{L}g} \tag{III}
\end{gather}
\]
onde mL é a massa de líquido deslocado pelo corpo.Substituindo as expressões (II) e (III) na expressão (I)
\[
\begin{gather}
mg-m_{L}g=ma \tag{IV}
\end{gather}
\]
A densidade é dada por
\[ \bbox[#99CCFF,10px]
{d=\frac{m}{V}}
\]
com o volume (V) do corpo igual ao volume do líquido deslocado, escrevendo essa expressão para o corpo
e o líquido
\[
\begin{gather}
d_{C}=\frac{m}{V}\\
m=d_{C}V \tag{V}
\end{gather}
\]
\[
\begin{gather}
d_{L}=\frac{m_{L}}{V}\\
m_{L}=d_{L}V \tag{VI}
\end{gather}
\]
substituindo as expressões (V) e (VI) na expressão (IV), obtemos a aceleração
\[
\begin{gather}
d_{C}Vg-d_{L}Vg=d_{C}Va\\
a=\frac{d_{C}Vg-d_{L}Vg}{d_{C}V}\\
a=\frac{\cancel{V}g(d_{C}-d_{L})}{d_{C}\cancel{V}}\\
a=\frac{g(d_{C}-d_{L})}{d_{C}} \tag{VII}
\end{gather}
\]
O corpo afunda sob a ação da aceleração dada pela expressão (VII), está em
Movimento Retilíneo Uniformemente Variado (M.R.U.V.), a expressão que rege este tipo de
movimento é dada por
\[ \bbox[#99CCFF,10px]
{S=S_{0}+v_{0}t+\frac{a}{2}t^{2}}
\]
\[
\begin{gather}
h=0+0.t+\frac{1}{2}\frac{g(d_{C}-d_{L})}{d_{C}}t^{2}\\
t^{2}=\frac{2hd_{C}}{g(d_{C}-d_{L})}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{t=\sqrt{\frac{2hd_{C}}{g(d_{C}-d_{L})}\;}}
\]
b) A energia cinética é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{E_{C}=\frac{mv^{2}}{2}} \tag{VIII}
\end{gather}
\]
A velocidade no Movimento Retilíneo Uniformemente Variado (M.R.U.V.) é dada por
\[ \bbox[#99CCFF,10px]
{v=v_{0}+at}
\]
substituindo a expressão (VII) para a aceleração e o tempo calculado no item anterior
\[
\begin{gather}
v=0+\frac{g(d_{C}-d_{L})}{d_{C}}\sqrt{\frac{2hd_{C}}{g(d_{C}-d_{L})}\;}\\
v=\sqrt{\frac{g^{\cancel{2}}(d_{C}-d_{L})^{\cancel{2}}}{d_{C}^{\cancel{2}}}\frac{2h\cancel{d_{C}}}{\cancel{g}\cancel{(d_{C}-d_{L})}}\;}\\
v=\sqrt{\frac{2hg(d_{C}-d_{L})}{d_{C}}\;} \tag{IX}
\end{gather}
\]
substituindo a expressão (IX) na expressão (VIII)
\[
\begin{gather}
E_{C}=\frac{m}{2}\left(\sqrt{\frac{2hg(d_{C}-d_{L})}{d_{C}}\;}\right)^{2}\\
E_{C}=\frac{m}{\cancel{2}}\frac{\cancel{2}hg(d_{C}-d_{L})}{d_{C}}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{E_{C}=\frac{mhg(d_{C}-d_{L})}{d_{C}}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .