Um cilindro circular reto, de altura h = 30 cm e área da base A = 10 cm2,
flutua na água, em posição vertical tendo 2/3 de sua altura imersa, aplica-se na direção axial da base
superior uma força F passando o cilindro a ter 5/6 de sua altura imersa. Determine:
a) Qual a densidade do cilindro relativa à água?
b) Qual a intensidade da força F?
Dados: g = 9,8 m/s2, densidade da água = 1 g/cm3.
Dados do problema:
- Altura do cilindro: h = 30 cm;
- Área da base do cilindro: A = 10 cm2;
- Fração da altura do cilindro inicialmente imersa: \( h_1=\dfrac{2}{3}h \);
- Fração da altura do cilindro imersa após aplicada a força: \( h_2=\dfrac{5}{6}h \);
- Aceleração da gravidade: g = 9,8 m/s2;
- Densidade da água: da = 1 g/cm3.
Solução:
Em primeiro lugar vamos converter a aceleração da gravidade dada em metros por segundo por segundo
(m/s2) para centímetros por segundo por segundo (cm/s2).
\[
\begin{gather}
g=9,8\;\frac{\cancel{\text{m}}}{\text{s}^{2}}.\frac{100\;\text{cm}}{1\;\cancel{\text{m}}}=980\;\text{cm/s}^{2}
\end{gather}
\]
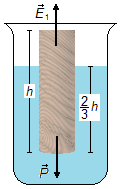
a) Na situação inicial atuam no cilindro a força peso
\( \vec{P} \)
e a força de empuxo
\( {\vec{E}}_1 \)
devido ao volume de água deslocada pela altura
h1 imersa do cilindro (Figura 1).
A força peso é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{P=mg} \tag{I}
\end{gather}
\]
A densidade é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{d=\frac{m}{V}}
\end{gather}
\]
\[
\begin{gather}
m=dV \tag{II}
\end{gather}
\]
substituindo a equação (II) para a massa na equação (I)
\[
\begin{gather}
P=dVg \tag{III}
\end{gather}
\]
O volume de um cilindro é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{V=Ah} \tag{IV}
\end{gather}
\]
substituindo a equação (IV) na equação (III)
\[
\begin{gather}
P=dAhg \tag{V}
\end{gather}
\]
A força de empuxo é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{E=m_{\small L}g} \tag{VI}
\end{gather}
\]
Usando a equação (II), onde mL = ma, a massa de água
deslocada será
\[
\begin{gather}
m_a=d_aV_a \tag{VII}
\end{gather}
\]
onde da é a densidade da água onde o corpo está imerso e Va é o volume
de água deslocada.
Substituindo a equação (VII) na equação (VI)
\[
\begin{gather}
E_1=d_aV_ag \tag{VIII}
\end{gather}
\]
usando a equação (IV) para o volume de água deslocada
\[
\begin{gather}
V_a=Ah_1 \tag{IX}
\end{gather}
\]
substituindo a equação (IX) para o volume de água deslocada na equação (VIII)
\[
\begin{gather}
E_1=d_aAh_1g \tag{X}
\end{gather}
\]
Como o corpo está em equilíbrio a força peso e a força de empuxo se anulam
\[
\begin{gather}
E_1=P \tag{XI}
\end{gather}
\]
substituindo as equações (V) e (X) na condição (XI)
\[
\begin{gather}
d_a\cancel Ah_1\cancel g=d\cancel Ah\cancel g \\[5pt]
d_ah_1=dh \\[5pt]
\frac{d}{d_a}=\frac{h_1}{h}
\end{gather}
\]
substituindo a altura do cilindro imersa na água, dado no problema
\[
\begin{gather}
\frac{d}{d_a}=\frac{\dfrac{2}{3}\cancel{h}}{\cancel{h}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\frac{d}{d_a}=\frac{2}{3}}
\end{gather}
\]
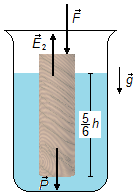
b) Na situação final temos a força externa
\( \vec{F} \)
atuando no cilindro. Adotamos um referencial para baixo, no mesmo sentido da aceleração da gravidade, para que o
cilindro permaneça em equilíbrio a somatória das forças deve ser nula (Figura 2).
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\sum F=0}
\end{gather}
\]
\[
\begin{gather}
P+F-E_2=0 \tag{XII}
\end{gather}
\]
o empuxo
\( {\vec{E}}_2 \)
é devido ao volume de água deslocada pela altura
h2 imersa do cilindro. Substituindo
as equações (V) e (X), para a altura
h2, na equação (XII)
\[
\begin{gather}
dAhg+F=d_aAh_2g \\[5pt]
F=d_aAh_2g-dAhg
\end{gather}
\]
substituindo a densidade do cilindro em relação à água
\( \left(d=\frac{2}{3}d_a\right) \)
encontrada no item anterior
\[
\begin{gather}
F=d_aA\frac{5}{6}hg-\frac{2}{3}d_aAhg \\[5pt]
F=d_aAhg\left(\frac{5}{6}-\frac{2}{3}\right)
\end{gather}
\]
multiplicando por 2 o numerador e o denominador do segundo termo entre parênteses
\[
\begin{gather}
F=d_aAhg\left(\frac{5}{6}-\frac{2}{3}.\frac{2}{2}\right) \\[5pt]
F=d_aAhg\left(\frac{5}{6}-\frac{4}{6}\right) \\[5pt]
F=\left(\frac{1}{6}\right)d_aAhg
\end{gather}
\]
substituindo os dados do problema
\[
\begin{gather}
F=\left(\frac{1}{6}\right).1.10.30.980\\[5pt]
F=50.980
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{F=49000\;\text{dinas}}
\end{gather}
\]
Observação: dina é a unidade de força no sistema CGS de unidades.
EN
