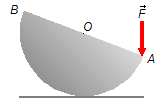
Uma semiesfera de peso P repousa sobre um plano horizontal liso. Na extremidade A do
diâmetro AB é aplicada uma força F que obriga a semiesfera a se inclinar de maneira que
AB passa formar com o plano horizontal um ângulo α. Calcular esse ângulo a sabendo que o
centro de gravidade da semiesfera encontra-se a uma distância do centro O igual a 3/8 do raio.
Dados do problema:
- Peso da semiesfera: P;
- Força aplicada: F;
- Raio da semiesfera: dOA=R;
- Posição do centro de gravidade: \( d_{cg}=\frac{3}{8}R \);
Esquema do problema:
O problema nos diz que o centro de gravidade da semiesfera está localizado a
\( \frac{3}{8} \)
de unidade a partir do ponto O (Figura 1-A).
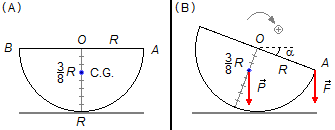
Consideramos a força peso
\( \vec{P} \)
concentrada nesse ponto e a força
\( \vec F \)
aplicada no ponto A a uma distância igual ao raio da semiesfera (Figura 1-B). Quando a força
\( \vec F \)
é aplicada a semiesfera se inclina até que o diâmetro AB forme um ângulo α em relação à
horizontal.
Adotamos o ponto O como origem do sistema de referência, vamos adotar o sentido horário como sendo
positivo.
Solução:
O momento de uma força é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{M=Fd} \tag{I}
\end{gather}
\]
“Esquecendo” a força
\( \vec F \),
a força peso
\( \vec{P} \),
pode ser decomposta em duas componentes, uma componente paralela ao raio que passa pelo centro de
gravidade
\( {\vec P}_{\small P} \)
e outra componente perpendicular ou normal
\( {\vec P}_{\small N} \).
O ângulo entre a horizontal e o segmento AB é dado igual à α, o ângulo entre o
segmento AB e a vertical que passa por O chamamos de β, então a soma de
α e β deve ser 90°, são ângulos complementares, então β deve ser
\( \alpha +\beta =90°\Rightarrow \beta =90°-\alpha \).
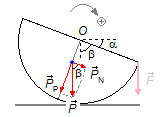
Figura 2
Como a componente normal da força peso está na mesma direção do segmento AB e a força peso é
vertical, o ângulo entre elas também é β, são ângulos correspondes. Apenas a componente normal
contribui para que a semiesfera gire em torno do ponto O, como esta componente faz girar no
sentido contrário da orientação escolhida o momento desta força será negativo, aplicando a expressão (I)
\[
\begin{gather}
M_{\small P_{\small N}}=-P_{\small N}d_{cg} \tag{II}
\end{gather}
\]
A componente normal da força peso é dada por
\[
\begin{gather}
P_{\small N}=P\cos\beta \\[5pt]
P_{\small N}=P\cos(90°-\alpha)
\end{gather}
\]
Da
Trigonometria
\[
\cos (a-b)=\cos a\,\cos b+\operatorname{sen}a\,\operatorname{sen}b
\]
\[
\begin{gather}
P_{\small N}=P(\cos 90°\cos\alpha+\operatorname{sen}90°\operatorname{sen}\alpha)\\[5pt]
P_{\small N}=P(0\times\cos\alpha+1\times\operatorname{sen}\alpha) \\[5pt]
P_{\small N}=P\operatorname{sen}\alpha \tag{III}
\end{gather}
\]
substituindo a expressão (III) na expressão (II)
\[
\begin{gather}
M_{P_{\small N}}=-P\,\operatorname{sen}\alpha\,d_{cg} \tag{IV}
\end{gather}
\]
“Esquecendo” a força peso
\( \vec{P} \),
a força
\( \vec F \),
pode ser decomposta em duas componentes, uma componente paralela ao raio que passa pelo centro O
\( {\vec F}_{\small P} \)
e outra componente perpendicular ou normal
\( {\vec F}_{\small N} \).
O ângulo entre a horizontal e o segmento AB é dado igual à α, o ângulo entre o segmento
AB e a vertical que passa por A chamamos de β, então a soma de α e β deve
ser 90°, são ângulos complementares, então β deve ser
\( \alpha +\beta =90°\Rightarrow \beta =90°-\alpha \).
Apenas a componente normal contribui para que a semiesfera gire em torno do ponto O, como esta
componente faz girar no mesmo sentido da orientação escolhida o momento desta força será positivo,
pela expressão (I)
\[
\begin{gather}
M_{\small F_{\small N}}=F_{\small N}\,d_{\small{OA}} \tag{V}
\end{gather}
\]
A componente normal da força é dada por
\[
\begin{gather}
F_{\small N}=F\operatorname{sen}\beta \\[5pt]
F_{\small N}=F\operatorname{sen}(90°-\alpha)
\end{gather}
\]
Da
Trigonometria
\[
\operatorname{sen}(a-b)=\operatorname{sen}a\,\cos b-\operatorname{sen}b\,\cos a
\]
\[
\begin{gather}
F_{\small N}=F\,(\operatorname{sen}90°\cos\alpha-\operatorname{sen}\alpha\cos 90°) \\[5pt]
F_{\small N}=F\,(1\times\cos\alpha-\operatorname{sen}\alpha\times 0) \\[5pt]
F_{\small N}=F\,\cos\alpha \tag{IV}
\end{gather}
\]
substituindo a expressão (VI) na expressão (V)
\[
\begin{gather}
M_{\small F_{\small N}}=F\cos\alpha\,d_{\small{OA}} \tag{VII}
\end{gather}
\]
Usando a condição de que a somatória dos momentos é nula
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\sum M=0} \tag{VIII}
\end{gather}
\]
substituindo as expressões (IV) e (VII) na condição (VIII)
\[
\begin{gather}
M_{\small P_{\small N}}+M_{\small F_{\small N}}=0 \\[5pt]
-P\,\operatorname{sen}\alpha d_{\small{OG}}+F\cos\alpha d_{\small{OA}}=0 \\[5pt]
-P\,\operatorname{sen}\alpha\frac{3}{8}R+F\cos\alpha R=0 \\[5pt]
F\cancel{R}\cos\alpha=\frac{3}{8}\cancel{R}\,P\operatorname{sen}\alpha \\[5pt]
\frac{\operatorname{sen}\alpha}{\cos\alpha}=\frac{8}{3}\frac{F}{P}
\end{gather}
\]
Da Trigonometria
\( \operatorname{tg}\alpha =\dfrac{\operatorname{sen}\alpha }{\cos \alpha } \)
\[
\begin{gather}
\operatorname{tg}\alpha=\frac{8}{3}\frac{F}{P}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\alpha =\operatorname{arc tg}\,\frac{8}{3}\frac{F}{P}}
\end{gather}
\]
EN
