Exercício Resolvido de Estática
publicidade
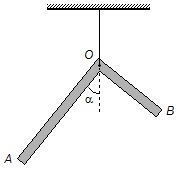
Uma barra AOB homogênea de seção transversal constante cujo peso é de 15 N é dobrada formando um
ângulo reto em O com AO=1 m e BO=0,5 m. Suspende-se a barra pelo ponto O.
Determinar:
a) O ângulo α formado por AO com a vertical na posição de equilíbrio;
b) A intensidade da força horizontal que deve ser aplicada em A, no plano AOB, para que AO e BO sejam igualmente inclinados em relação à horizontal;
c) No caso do item (b), encontre a intensidade reação no ponto de suspensão O.
a) O ângulo α formado por AO com a vertical na posição de equilíbrio;
b) A intensidade da força horizontal que deve ser aplicada em A, no plano AOB, para que AO e BO sejam igualmente inclinados em relação à horizontal;
c) No caso do item (b), encontre a intensidade reação no ponto de suspensão O.
Dados do problema:
- Peso da barra: P=15 N;
- Comprimento do segmento AO: DA=1 m;
- Comprimento do segmento BO: DB=0,5 m.
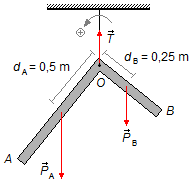
Adotamos o ponto O, onde a peça está fixa, como ponto de referência. Como a barra é homogênea e
de seção constante sua massa está igualmente distribuída por toda a sua extensão, assim podemos
considerar que o centro de massa de cada um dos “braços” da peça está em seu centro. Em AO o
centro está em
\( d_{A}=\frac{D_{A}}{2}=\frac{1}{2}=0,5\;\text{m} \),
onde está aplicada a força peso
\( \vec{P}_{A} \).
Em BO o centro está em
\( d_{B}=\frac{D_{B}}{2}=\frac{0,5}{2}=0,25\;\text{m} \),
onde está aplicada a força peso
\( {\vec{P}}_{B} \).
No ponto O temos a força de tensão
\( \vec{T} \)
(Figura 1).
A peça pode girar em torno do ponto O, vamos adotar o sentido anti-horário como sendo positivo.
Como a barra está dobrada numa proporção 2:1, ou seja, um “braço” tem o dobro do comprimento do outro (1 m e 0,5 m), e como a barra é homogênea, seu peso está distribuído na mesma proporção. Assim do total de 15 N, PA=10 N e PB=5 N.
A peça pode girar em torno do ponto O, vamos adotar o sentido anti-horário como sendo positivo.
Como a barra está dobrada numa proporção 2:1, ou seja, um “braço” tem o dobro do comprimento do outro (1 m e 0,5 m), e como a barra é homogênea, seu peso está distribuído na mesma proporção. Assim do total de 15 N, PA=10 N e PB=5 N.
Solução
a) O momento de uma força é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{M=Fd} \tag{I}
\end{gather}
\]
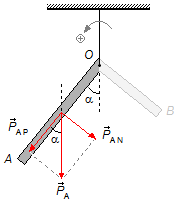
“Esquecendo” o segmento BO da peça e considerando apenas o segmento AO, a força peso
\( {\vec P}_{A} \)
pode ser decomposta em duas componentes, uma componente paralela ao “braço”
\( {\vec P}_{AP} \)
e outra componente perpendicular ou normal
\( {\vec P}_{AN} \).
O ângulo entre o segmento AO e a vertical por O é dada igual à α, a força peso \( {\vec P}_{A} \) é paralela à vertical que passa por O e a componente \( {\vec P}_{AP} \) está na mesma direção que o segmento AO, então o ângulo entre a força peso e a componente paralela também vale α, são ângulos correspondes (Figura 2).
Apenas a componente normal contribui para que o “braço” gire em torno do ponto O, como esta componente faz girar no mesmo sentido da orientação escolhida o momento desta força será positivo, aplicando a expressão (I)
O ângulo entre o segmento AO e a vertical por O é dada igual à α, a força peso \( {\vec P}_{A} \) é paralela à vertical que passa por O e a componente \( {\vec P}_{AP} \) está na mesma direção que o segmento AO, então o ângulo entre a força peso e a componente paralela também vale α, são ângulos correspondes (Figura 2).
Apenas a componente normal contribui para que o “braço” gire em torno do ponto O, como esta componente faz girar no mesmo sentido da orientação escolhida o momento desta força será positivo, aplicando a expressão (I)
\[
\begin{gather}
M_{P_{AN}}=P_{AN}d_{A} \tag{II}
\end{gather}
\]
A compoente normal é dada por (Figura 2)
\[
\begin{gather}
P_{AN}=P_{A}\operatorname{sen}\alpha \tag{III}
\end{gather}
\]
substituindo a expressão (III) na expressão (II)
\[
\begin{gather}
M_{P_{AN}}=P_{A}\operatorname{sen}\alpha d_{A} \tag{IV}
\end{gather}
\]
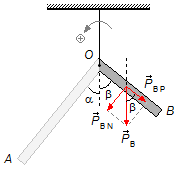
“Esquecendo” o segmento AO da peça e considerando apenas o segmento BO, a força peso
\( {\vec P}_{B} \)
pode ser decomposta em duas componentes, uma componente paralela ao “braço”
\( {\vec P}_{BP} \)
e outra componente perpendicular ou normal
\( {\vec P}_{BN} \).
O ângulo entre o segmento BO e a vertical por O chamamos de β, a força peso \( {\vec P}_{B} \) é paralela à vertical que passa por O e a componente \( {\vec P}_{BP} \) está na mesma direção que o segmento BO, então o ângulo entre a força peso e a componente paralela também vale β, são ângulos correspondes (Figura 3). Como a barra foi dobrada com um ângulo reto (90°) em O a soma de α e β deve ser 90°, são ângulos complementares, então β deve ser \( \alpha +\beta =90°\Rightarrow \beta=90°-\alpha \).
Apenas a componente normal contribui para que o “braço” gire em torno do ponto O, como esta componente faz girar no sentido contrário da orientação escolhida o momento desta força será negativo, aplicando a expressão (I)
O ângulo entre o segmento BO e a vertical por O chamamos de β, a força peso \( {\vec P}_{B} \) é paralela à vertical que passa por O e a componente \( {\vec P}_{BP} \) está na mesma direção que o segmento BO, então o ângulo entre a força peso e a componente paralela também vale β, são ângulos correspondes (Figura 3). Como a barra foi dobrada com um ângulo reto (90°) em O a soma de α e β deve ser 90°, são ângulos complementares, então β deve ser \( \alpha +\beta =90°\Rightarrow \beta=90°-\alpha \).
Apenas a componente normal contribui para que o “braço” gire em torno do ponto O, como esta componente faz girar no sentido contrário da orientação escolhida o momento desta força será negativo, aplicando a expressão (I)
\[
\begin{gather}
M_{P_{BN}}=-P_{BN}d_{B} \tag{V}
\end{gather}
\]
A componente normal será dada por (Figura 3)
\[
\begin{gather}
P_{BN}=P_{BA}\operatorname{sen}\beta\\[5pt]
P_{BN}=P_{B}\operatorname{sen}(90°-\alpha)
\end{gather}
\]
Lembrando da Trigonometria
\( \sin (a-b)=\operatorname{sen}a\,\cos b-\sin b\,\cos a \)
\[ \sin (a-b)=\operatorname{sen}a\,\cos b-\sin b\,\cos a \]
\[
\begin{gather}
P_{BN}=P_{B}(\operatorname{sen}90°\cos \alpha -\operatorname{sen}\alpha \cos 90°)\\[5pt]
P_{BN}=P_{B}(1.\cos \alpha -\operatorname{sen}\alpha .0)\\[5pt]
P_{BN}=P_{B}\cos \alpha \tag{VI}
\end{gather}
\]
substituindo a expressão (VI) na expressão (V)
\[
\begin{gather}
M_{P_{BN}}=-P_{B}\cos \alpha d_{B} \tag{VII}
\end{gather}
\]
No ponto O temos a força de tensão, aplicando (I)
\[
\begin{gather}
M_{T}=Td_{T}
\end{gather}
\]
como a distância é nula em relação à origem,
\( d_{T}=0 \),
a força está aplicada na própria origem
\[
\begin{gather}
M_{T}=T.0\\[5pt]
M_{T}=0 \tag{VIII}
\end{gather}
\]
Usando a condição de que a somatória dos momentos é nula
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\sum M=0} \tag{IX}
\end{gather}
\]
substituindo as expressões (IV), (VII) e (VIII) na condição (IX)
\[
\begin{gather}
M_{P_{AN}}+M_{P_{BN}}+M_{T}=0\\[5pt]
P_{A}\operatorname{sen}\alpha d_{A}-P_{B}\cos \alpha d_{B}+0=0\\[5pt]
P_{A}\operatorname{sen}\alpha d_{A}=P_{B}\cos \alpha d_{B}\\[5pt]
\frac{\operatorname{sen}\alpha }{\cos \alpha}=\frac{P_{B}d_{B}}{P_{A}d_{A}}
\end{gather}
\]
Lembrando da Trigonometria
\( \operatorname{tg}\alpha =\frac{\operatorname{sen}\alpha }{\cos \alpha } \)
substituindo os dados do problema
\[
\begin{gather}
\operatorname{tg}\alpha =\frac{5.0,25}{10.0.5}\\[5pt]
\operatorname{tg}\alpha =\frac{1,25}{5}\\[5pt]
\operatorname{tg}\alpha =0,25\\[5pt]
\alpha =\operatorname{arc tg}\,0,25
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\alpha \simeq 14°}
\end{gather}
\]
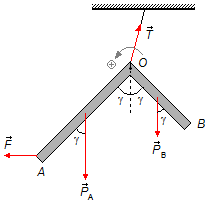
b) Uma força
\( \vec{F} \)
aplicada no ponto A faz a peça girar em torno do ponto O até que os ângulos entre os
dois segmentos fiquem iguais a γ, a peça também é puxada para a esquerda de modo que o fio de
fixação no teto deixa de estar num posição vertical (Figura 4).
Observação: Na condição do item (a) o ângulo α entre o segmento AO e a
vertical foi determinado como sendo 14°, portanto o ângulo entre o segmento BO e a vertical vale
\( 90°-14°=76° \).
Para que os dois ângulos fiquem iguais, a peça deve girar de modo que o ângulo de 14° aumente e o de 76°
diminua (até ficarem iguais a 45°), isto acontece quando a peça gira no sentido horário, não confundir
com a seta da Figura 4 que indica apenas o sentido positivo do sistema de referência.
Considerando apenas o segmento AO, a força
\( \vec{F} \)
pode ser decomposta em duas componentes, uma componente paralela ao “braço”
\( {\vec{F}}_{P} \)
e outra componente perpendicular ou normal
\( {\vec{F}}_{N} \).
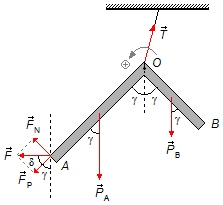
O ângulo entre o segmento AO e a vertical por O é γ, o ângulo entre a vertical que passa pelo ponto A e a componente paralela à AO também é γ, são ângulos correspondentes. Como a força aplicada é horizontal ela forma um ângulo δ com a componente paralela, a soma de γ e δ deve ser 90° (são ângulos complementares) \( \gamma +\delta =90°\Rightarrow \delta =90°-\gamma \) (Figura 5).
Apenas a componente normal contribui para que o “braço” gire em torno do ponto O, como esta componente faz girar no sentido contrário da orientação escolhida o momento desta força será negativo, pela expressão (I), onde a distância do ponto de referência O ao ponto de aplicação da força é o comprimento do segmento AO dado no problema
O ângulo entre o segmento AO e a vertical por O é γ, o ângulo entre a vertical que passa pelo ponto A e a componente paralela à AO também é γ, são ângulos correspondentes. Como a força aplicada é horizontal ela forma um ângulo δ com a componente paralela, a soma de γ e δ deve ser 90° (são ângulos complementares) \( \gamma +\delta =90°\Rightarrow \delta =90°-\gamma \) (Figura 5).
Apenas a componente normal contribui para que o “braço” gire em torno do ponto O, como esta componente faz girar no sentido contrário da orientação escolhida o momento desta força será negativo, pela expressão (I), onde a distância do ponto de referência O ao ponto de aplicação da força é o comprimento do segmento AO dado no problema
\[
\begin{gather}
M_{F_{N}}=-F_{N}D_{A} \tag{X}
\end{gather}
\]
A componente normal será dada por (Figura 5)
\[
\begin{gather}
F_{N}=F\operatorname{sen}\delta\\[5pt]
F_{N}=F\operatorname{sen}(90°-\gamma)
\end{gather}
\]
usando a propriedade do seno da diferença acima
\[
\begin{gather}
F_{N}=F(\operatorname{sen}90°\cos \gamma -\operatorname{sen}\gamma \cos 90°)\\[5pt]
F_{N}=F(1.\cos \gamma -\operatorname{sen}\gamma .0)\\[5pt]
F_{N}=F\cos \gamma \tag{XI}
\end{gather}
\]
substituindo a expressão (XI) na expressão (X)
\[
\begin{gather}
M_{F_{N}}=-F\cos \gamma D_{A} \tag{XII}
\end{gather}
\]
Para as outras forças envolvidas no sistema continuam válidas as expressões anteriores com a mudança do
ângulo α em (IV) e (VII) pelo novo ângulo γ. Substituindo (IV), (VII), (VIII) e (XII) na
condição (IX)
\[
\begin{gather}
M_{P_{AN}}+M_{P_{BN}}+M_{T}+M_{F_{N}}=0\\[5pt]
P_{A}\operatorname{sen}\gamma d_{A}-P_{B}\cos \gamma d_{B}+0-F\cos \gamma D_{A}=0\\[5pt]
P_{A}\operatorname{sen}\gamma d_{A}=P_{B}\cos \gamma d_{B}+F\cos \gamma D_{A}
\end{gather}
\]
colocando cos γ em evidência do lado direito da igualdade
\[
\begin{gather}
P_{A}\operatorname{sen}\gamma d_{A}=\cos \gamma (P_{B}d_{B}+FD_{A})
\end{gather}
\]
a barra é dobrada formando um ângulo de 90°, e queremos que os dois lados tenham a mesma inclinação
\( \gamma =45° \)
Lembrando da Trigonometria
\( \cos 45°=\operatorname{sen}45°=\frac{\sqrt{2\,}}{2} \)
\[
\begin{gather}
P_{A}d_{A}\cancel{\frac{\sqrt{2\,}}{2}}=\cancel{\frac{\sqrt{2\,}}{2}}(P_ {B}d_{B}+FD_{A})
P_{A}d_{A}=P_{B}d_{B}+FD_{A}\\[5pt]
F=\frac{P_{A}d_{A}-P_{B}d_{B}}{D_{A}}
\end{gather}
\]
substituindo os valores dados
\[
\begin{gather}
F=\frac{10.0,5-5.0,25}{1}\\[5pt]
F=5-1,25
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{F=3,75\;\text{N}}
\end{gather}
\]
c) Desenhando as forças que atuam no sistema da Figura 5 em um sistema de eixos coordenados xy
temos o esquema mostrado na Figura 6. Para que o sistema permaneça em equilíbrio aplicamos a condição de que a
somatória das forças é nula
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\sum F=0} \tag{XIII}
\end{gather}
\]
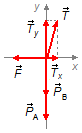
Direção x:
- \( {\vec T}_{x} \): componente da força de tensão na direção x;
- \( \vec{F} \): força externa aplicada para equilibrar a barra.
\[
\begin{gather}
T_{x}-F=0\\[5pt]
T_{x}=F
\end{gather}
\]
usando o resultado do item (b)
\[
\begin{gather}
T_{x}=3,75\;\text{N} \tag{XIV}
\end{gather}
\]
Direção y:
- \( {\vec T}_{y} \): componente da força de tensão na direção y;
- \( {\vec P}_{A} \): força peso do segmento AO;
- \( {\vec P}_{B} \): força peso do segmento BO.
\[
\begin{gather}
T_{y}-P_{A}-P_{B}=0\\[5pt]
T_{y}=P_{A}+P_{B}
\end{gather}
\]
substituindo os dados do problema
\[
\begin{gather}
T_{y}=10+5 \\[5pt]
T_{y}=15\;N \tag{XV}
\end{gather}
\]
A reação à tensão será dada pelo Teorema de Pitágoras (Figura 6)
\[
\begin{gather}
T^{2}=T_{x}^{2}+T_{y}^{2}
\end{gather}
\]
substituindo as expressões (XIV) e (XV)
\[
\begin{gather}
T^{2}=3,75^{2}+15^{2}\\[5pt]
T^{2}=14,1+225\\[5pt]
T^{2}=239,1\\[5pt]
T=\sqrt{239,1\;}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T\simeq 15,4\;\text{N}}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .