Exercício Resolvido de Energia, Trabalho e Potência
publicidade
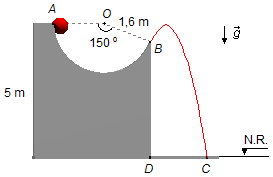
Um corpo de massa 100 g é abandonado no ponto A sobre uma superfície cilíndrica, com abertura de 150°, sem atrito, cujo o eixo é horizontal e normal ao plano da figura em O. Os pontos A e O estão sobre o mesmo nível a 5 m acima do solo e o raio da superfície mede 1,6 m. Ao atingir o ponto B o corpo abandona a superfície e atinge o solo no ponto C.

Determinar:
a) O módulo da velocidade do corpo no ponto B;
b) O módulo da velocidade do corpo no ponto C;
c) A distância CD;
d) As energias cinética, potencial e mecânica total no ponto A;
e) As energias cinética, potencial e mecânica total no ponto B;
f) As energias cinética, potencial e mecânica total no ponto C.
Adote g = 10 m/s2.
Dados do problema:
- Massa do corpo: m = 100 g;
- Raio da superfície cilíndrica: r = 1,6 m;
- Ângulo de abertura da superfície: θ = 150°;
- Altura inicial do corpo: hA = 5 m;
- Aceleração da gravidade: g = 10 m/s2.
Adotamos um Nível de Referência (N.R.) no solo. O corpo é abandonado com a velocidade
inicial nula em A, vA = 0, ele desliza pela superfície
cilíndrica até o ponto B, onde abandona a superfície descrevendo uma trajetória parabólica como
um projétil até o ponto C (Figura 1).
Solução
Em primeiro lugar devemos converter a massa do corpo dada em gramas (g) para quilogramas (kg) usado no Sistema Internacional (S.I.)
\[
\begin{gather}
m=100\;\cancel{\text{g}}.\frac{1\;\text{kg}}{1000\;\cancel{\text{g}}}=1.10^{2}.\frac{1\;\text{kg}}{1.10^{3}}=1.10^{2}.10^{-3}\;\text{kg}=1.10^{-1}\;\text{kg}=0,1\;\text{kg}
\end{gather}
\]
a) Para determinarmos a velocidade no ponto B usamos o Princípio da Conservação da Energia,
a energia mecânica no ponto A deve ser igual à energia em B. No ponto A o corpo possui
apena Energia Potencial devido a altura em relação ao nível de referência, a Energia Cinética
é igual a zero, inicialmente o corpo está em repouso. No ponto B o corpo possui
Energia Potencial devido a altura em relação ao nível de referência e Energia Cinética devido
a velocidade que ele possui
\[
\begin{gather}
E_{M}^{A}=E_{M}^{B}\\[5pt]
E_{P}^{A}=E_{P}^{B}+E_{C}^{B}
\end{gather}
\]
a Energia Cinética é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{E_{C}=\frac{mv^{2}}{2}}
\end{gather}
\]
a Energia Potencial é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{E_{P}=mgh}
\end{gather}
\]
\[
\begin{gather}
\cancel{m}gh_{A}=\cancel{m}gh_{B}+\frac{\cancel{m}v_{B}^{2}}{2}\\{5pt}
gh_{A}=gh_{B}+\frac{v_{B}^{2}}{2} \tag{I}
\end{gather}
\]
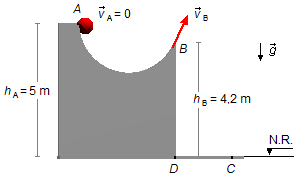
Pela Figura 2
\[
\begin{gather}
h_{A}=h+h_{B}
\end{gather}
\]
portanto a altura do ponto B será de
\[
\begin{gather}
h_{B}=h_{A}-h \tag{II}
\end{gather}
\]
O segmento
\( \overline{{OP}} \)
é horizontal, como o ângulo de abertura da superfície cilíndrica é de 150°, o ângulo
\( P\hat{O}B \)
será de 30° (180°−150°=30°).

Como o segmento \( \overline{{OB}} \) é um raio do cilindro e representa a hipotenusa do triângulo ΔPOB
\[
\begin{gather}
\operatorname{sen}30°=\frac{\text{cateto oposto}}{\text{hipotenusa}}=\frac{h}{r}
\end{gather}
\]
da Trigonometria temos que
\( \operatorname{sen}30°=\frac{1}{2} \)
\[
\begin{gather}
\frac{1}{2}=\frac{h}{1,6}\\[5pt]
h=\frac{1,6}{2}\\[5pt]
h=0,8\;\text{m} \tag{III}
\end{gather}
\]
substituindo a expressão (III) na expressão (II) e a altura do ponto A dada no problema, a altura
do ponto B será de
\[
\begin{gather}
h_{B}=5-0,8\\[5pt]
h_{B}=4,2\;\text{m} \tag{IV}
\end{gather}
\]
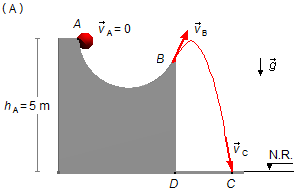
substituindo a expressão (IV) na expressão (I) e os dados do problema (Figura 3)
\[
\begin{gather}
10.5=10.4,2+\frac{v_{B}^{2}}{2}\\[5pt]
50=42+\frac{v_{B}^{2}}{2}\\[5pt]
50-42=\frac{v_{B}^{2}}{2}\\[5pt]
v_{B}^{2}=2.8\\[5pt]
v_{B}^{2}=16\\[5pt]
v_{B}=\sqrt{16\;}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_{B}=4\;\text{m/s}}
\end{gather}
\]
b) Para determinarmos a velocidade no ponto C usamos o Princípio da Conservação da Energia, a energia mecânica no ponto A deve ser igual à energia em C. No ponto A temos a mesma situação do item (a), no ponto C o corpo possui enercia cinética devido a velocidade e a Energia Potencial é nula, a altua em relação ao nível de referência é zero, hC = 0
\[
\begin{gather}
E_{M}^{A}=E_{M}^{C}\\[5pt]
E_{P}^{A}+E_{C}^{A}=E_{P}^{C}+E_{C}^{C}\\[5pt]
\cancel{m}gh_{A}=\frac{\cancel{m}v_{C}^{2}}{2}\\[5pt]
gh_{A}=\frac{v_{C}^{2}}{2} \tag{V}
\end{gather}
\]
substituindo os dados do problema
\[
\begin{gather}
10.5=\frac{v_{C}^{2}}{2}\\[5pt]
50=\frac{v_{C}^{2}}{2}\\[5pt]
v_{C}^{2}=2.50\\[5pt]
v_{C}^{2}=100\\[5pt]
v_{C}=\sqrt{100\;}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_{C}=10\;\text{m/s}}
\end{gather}
\]
c) No ponto B o movimento pode ser decomposto nas direções x e y. Pela Figura 5-B vemos que no movimento ao longo da direção x temos que para intervalos de tempos iguais temos intervalos de espaços iguais (Δx1 = Δx2 = Δx3 = Δx4 = Δx5). Na direção y temos que durante a subida para intervalos de tempos iguais temos intervalos de espaços menores, pois a esfera está sendo freada pela ação da gravidade (Δy1 > Δy2) até que a velocidade vy seja igual a zero, e então a gravidade puxa o corpo de volta em direção ao solo com velocidade acelerada, assim para intervalos de tempos iguais temos intervalos de espaços cada vez maiores (Δy3 < Δy4 < Δy5).

A velocidade no ponto B pode ser decomposta ao longo dos eixos x e y. A velocidade inicial vB, com que a esfera deixa a superfície, tem componentes nas direções x e y (Figura 5-A)
\[
\begin{gather}
v_{Bx}=v_{B}\cos 60°\\[10pt]
v_{By}=v_{B}\operatorname{sen}60°
\end{gather}
\]
Da Trigonometria temos que
\( \cos 60°=\frac{1}{2} \)
e
\( \operatorname{sen}60°=\frac{\sqrt{3\;}}{2} \)
e usando o valor de vB obtido no item (a)
\[
\begin{gather}
v_{Bx}=4.\frac{1}{2}\\[5pt]
v_{Bx}=2\;\text{m/s} \tag{VI}
\end{gather}
\]
\[
\begin{gather}
v_{By}=4.\frac{\sqrt{3\;}}{2}v_{B}\\[5pt]
v_{By}=2\sqrt{3\;}\;\text{m/s} \tag{VII}
\end{gather}
\]
Da decomposição do movimento vemos que na direção x não há aceleração atuando sobre a esfera, então
ela está em Movimento Uniforme (M.U.) e seu movimento é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S_{x}=S_{0x}+v_{x}t}
\end{gather}
\]
como no movimento uniforme vx = vBx é constante podemos substituir
vx pelo valor encontrado em (VI) e S0x = 0
\[
\begin{gather}
S_{x}=0+2t\\[5pt]
S_{x}=2t \tag{VIII}
\end{gather}
\]
Na direção y a esfera está sob a ação da aceleração da gravidade, portanto está em queda livre dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S_{y}=S_{0y}+v_{By}t-\frac{g}{2}t^{2}}
\end{gather}
\]
o sinal de negativo indica que a aceleração da gravidade está contra a orientação do referencial,
substituindo vBy pelo valor encontrado em (VII) e S0y = 4,2 m
\[
\begin{gather}
S_{y}=4,2+2\sqrt{3\;}t-10\frac{t^{2}}{2}\\[5pt]
S_{y}=4,2+2\sqrt{3\;}t-5t^{2} \tag{IX}
\end{gather}
\]
Quando o corpo atinge o solo no ponto C, que está no Nível de Referência, temos que o espaço
final ao longo do eixo-y é nulo (Sy = 0)
\[
\begin{gather}
-5t^{2}+2\sqrt{3\;}t+4,2=0
\end{gather}
\]
esta é uma Equação do 2.º Grau onde a incógnita é o valor de t
Solução de \( -5t^{2}+2\sqrt{3\;}t+4,2=0 \)
\[
\begin{gather}
\Delta=b^{2}-4ac=(2\sqrt{3\;}\;)^{2}-4.(-5).4,2=4.3+20.4,2=12+84=96\\[10pt]
t=\frac{-b\pm\sqrt{\Delta }}{2a}=\frac{-2\sqrt{3\;}\pm\sqrt{96\;}}{2.\left(-5\right)}=\frac{-2.1,73\pm 9,80}{-10}=\frac{-3,46\pm 9,80}{-10}
\end{gather}
\]
onde a raízes serão
\[
\begin{gather}
t_{1}=\frac{-3,46+9,80}{-10}=-0,6\\
\text{e}\\
t_{2}=\frac{-3,46-9,80}{-10}=1,3
\end{gather}
\]
Desprezando a primeira raiz que tem valor negativo (t1 < 0), o intervalo tempo para a esfera atingir o chão será t = 1,3 s. Como o intervalo de tempo para a esfera subir e descer é o mesmo que ela leva para ir percorrer a distância CD ao longo do eixo-x, substituindo este intervalo de tempo na expressão (VIII)
\[
\begin{gather}
S_{x}=2.1,3
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{S_{x}=2,6\;\text{m}}
\end{gather}
\]
d) Energia Cinética no ponto A
\[
\begin{gather}
E_{C}^{A}=\frac{mv_{A}^{2}}{2}\\[5pt]
E_{C}^{A}=\frac{0,1.0^{2}}{2}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{E_{C}^{A}=0\;\text{J}}
\end{gather}
\]
Energia Potencial no ponto A
\[
\begin{gather}
E_{P}^{A}=mgh_{A}\\[5pt]
E_{P}^{A}=0,1.10.5
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{E_{P}^{A}=5\;\text{J}}
\end{gather}
\]
Energia Mecânica Total no ponto A
\[
\begin{gather}
E_{M}^{A}=E_{C}^{A}+E_{P}^{A}\\[5pt]
E_{M}^{A}=0+5
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{E_{M}^{A}=5\;\text{J}}
\end{gather}
\]
e) Energia Cinética no ponto B
\[
\begin{gather}
E_{C}^{B}=\frac{mv_{B}^{2}}{2}\\[5pt]
E_{C}^{B}=\frac{0,1.4^{2}}{2}\\[5pt]
E_{C}^{B}=\frac{0,1.16}{2}\\[5pt]
E_{C}^{B}=\frac{1,6}{2}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{E_{C}^{B}=0,8\;\text{J}}
\end{gather}
\]
Energia Potencial no ponto B
\[
\begin{gather}
E_{P}^{B}=mgh_{B}\\[5pt]
E_{P}^{B}=0,1.10.4,2
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{E_{P}^{B}=4,2\;\text{J}}
\end{gather}
\]
Energia Mecânica Total no ponto B
\[
\begin{gather}
E_{M}^{B}=E_{C}^{B}+E_{P}^{B}\\[5pt]
E_{M}^{B}=0,8+4,2
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{E_{M}^{B}=5\;\text{J}}
\end{gather}
\]
f) Energia Cinética no ponto C
\[
\begin{gather}
E_{C}^{C}=\frac{mv_{C}^{2}}{2}\\[5pt]
E_{C}^{C}=\frac{0,1.10^{2}}{2}\\[5pt]
E_{C}^{C}=\frac{0,1.100}{2}\\[5pt]
E_{C}^{C}=\frac{10}{2}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{E_{C}^{C}=5\;\text{J}}
\end{gather}
\]
Energia Potencial no ponto C
\[
\begin{gather}
E_{P}^{C}=mgh_{C}\\[5pt]
E_{P}^{C}=0,1.10.0
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{E_{P}^{C}=0\;\text{J}}
\end{gather}
\]
Energia Mecânica Total no ponto C
\[
\begin{gather}
E_{M}^{C}=E_{C}^{C}+E_{P}^{C}\\[5pt]
E_{M}^{C}=5+0
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{E_{M}^{C}=5\;\text{J}}
\end{gather}
\]
Observação: Nos pontos A, B e C as energias cinética e potencial têm
valores diferentes dependendo das velocidades e das alturas, respectivamente, mas a energia mecânica total é
sempre a mesma, uma vez que não há perdas e dissipações.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .