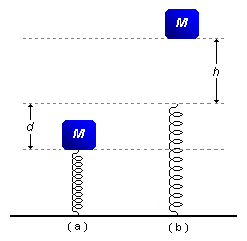
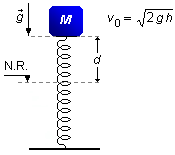
Na figura, a mola é ideal, a situação (a) é de equilíbrio estável do sistema massa-mola, e a situação (b) é a da mola em repouso. Abandonando-se o bloco M como indica a situação (b), determinar:
a) A constante elástica da mola;
b) A velocidade máxima atingida pelo bloco M.

Dados do problema:

• Altura da queda do bloco M até atingir a mola: h;
• Distância que a mola é comprimida sob ação do bloco M: d.

Solução:

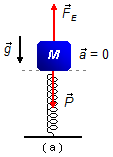
a) Para o cálculo da constante elástica da mola usamos a situação de equilíbrio mostrada em (a), Figura 1. As forças que atuam no bloco são:

• \( {\vec F}_e \): força elástica devido à mola;
• \( \vec P \): peso do bloco M.

Como o sistema está em equilíbrio, a soma de todas as forças que atuam sobre o bloco é igual a zero.

\[ \begin{gather} \bbox[#99CCFF,10px] {\sum F=0} \end{gather} \]

adotando-se um sistema de referência orientado para baixo e aplicando esta condição à Figura 1

\[ \begin{gather} P-F_e=0 \tag{I} \end{gather} \]

Figura 1

a força peso é dada por

a força elástica da mola é dada por

substituindo as equações (II) e (III) na equação (I) e x=d

a constante da mola será

b) Para calcular a velocidade máxima atingida pelo bloco, dividimos o problema em duas partes; em primeiro lugar a queda do bloco M até atingir a mola e em segundo a compressão da mola até a posição de equilíbrio.
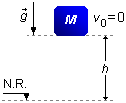
Na primeira parte o bloco está em queda livre, sob a ação da aceleração da gravidade partindo do repouso. Nestas condições podemos utilizar o Princípio da Conservação da Energia Mecânica. Tomando-se o Nível de Referência (N.R.) para esta parte do movimento na plataforma da mola. No ponto de onde o bloco é solto só temos Energia Potencial, \( E_p^i \), devido a altura em relação ao referencial, e no ponto onde o bloco bate na mola só temos Energia Cinética, \( E_c^f \), devido a velocidade (Figura 2)

\[ \begin{gather} E_m^i=E_m^f \\[5pt] E_p^i=E_c^f \tag{IV} \end{gather} \]

a Energia Potencial é dada por

\[ \begin{gather} \bbox[#99CCFF,10px] {E_p=mgh} \tag{V} \end{gather} \]

Figura 2

a Energia Cinética é dada por

substituindo as equações (V) e (VI) na equação (IV)

Na segunda parte (Figura 3-a) vemos que no momento em que o bloco bate na mola estão atuando no bloco a força peso e a força elástica da mola, ainda pequena, e que aumenta com a compressão da mola, neste ponto a aceleração do bloco é positiva (a>0) e a velocidade também é positiva (v>0). A medida que o bloco comprime a mola a força elástica aumenta até se igualar à força peso (Figura 3-b), neste ponto como as duas forças se equivalem a aceleração é zero (ponto de equilíbrio estável dado no problema) e a velocidade atingiu seu valor máximo (valor pedido no problema).

Figura 3

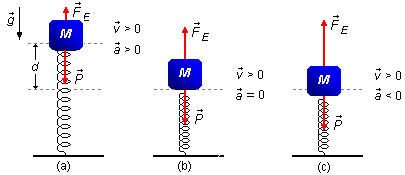
Na Figura 3-c o bloco passou do ponto de equilíbrio estável, a força elástica da mola supera o valor da força peso e a resultante das forças é "para cima", a aceleração "muda de sinal" (a<0), mas a velocidade continua "para baixo" (v>0) ela começa a diminuir em relação ao valor máximo atingido na situação anterior.

Então a posição em que a velocidade do bloco é máxima é a posição de equilíbrio, para calcular a sua velocidade neste ponto vamos utilizar novamente o Princípio da Conservação da Energia Mecânica (Figura 4). Adotando-se o nível de referência na altura de equilíbrio, temos que no ponto inicial (onde o bloco bate na mola) há Energia Potencial, \( E_p^i \), devido à altura d em relação ao nível de referência, e Energia Cinética, \( E_c^i \), devido à velocidade inicial v₀ dado pelo valor (VII) calculado acima. No ponto d, adotado como referência, a Energia Potencial é zero (não há altura), mas temos Energia Cinética, \( E_c^f \), devido a máxima velocidade do bloco e Energia Potencial Elástica, \( E_e \), devido a compressão da mola.

\[ \begin{gather} E_m^i=E_m^f \\[5pt] E_c^i+E_p^i=E_c^f+E_e \end{gather} \]

Figura 4

as energias potencial e cinética são dadas pelas equações (V) e (VI) respectivamente e a energia potencial elástica é dada por

substituindo as equações (V), (VI) e (VIII) para as situações inicial e final, e usando o valor de k calculado no item (a) e x=d