Exercício Resolvido de Resistores
publicidade
Encontre a resistência equivalente do circuito representado na figura. Dados: R1 = 2 Ω e R2 = 4 Ω.
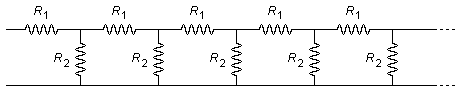
Dados do problema:
- R1 = 2 Ω;
- R2 = 4 Ω.
O circuito representa uma associação de infinitos resistores, vamos chamar o resistor equivalente entre os pontos A e B de X (Figura 1).
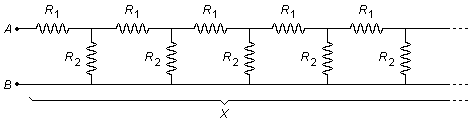
Se separarmos os dois primeiros resistores à esquerda, a associação que sobra à direita dos pontos A' e B', destacada em vermelho na Figura 2, é igual ao circuito original do problema.
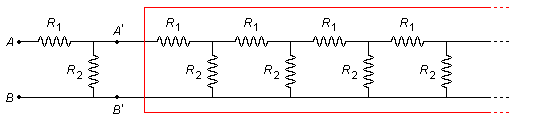
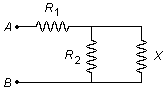
A resistência equivalente à direita de A' e B' também vale X e o circuito pode ser representado de maneira finita pelo seguinte esquema da Figura 3.
Temos dois resistores em paralelo (R2 e X) em série com o resistor R1.
A resistência equivalente de dois resistores em paralelo, Rpar, é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{R_{par}=\frac{R_{A}R_{B}}{R_{A}+R_{B}}}
\end{gather}
\]
com RA = R2 e RB = X. Somando este valor ao
resistor R1 em série obtemos o valor da resistência equivalente X do problema
\[
\begin{gather}
X=R_{1}+\frac{R_{2}X}{R_{2}+X}
\end{gather}
\]
substituindo os valores fornecidos pelo problema para R1 e R2
\[
\begin{gather}
X=2+\frac{4X}{4+X}
\end{gather}
\]
multiplicando todos os membros da equação por (4+X)
\[
\begin{gather}
X(4+X)=2(4+X)+\frac{4X}{4+X}(4+X)\\[5pt]
4X+X^{2}=8+2X+4X\\[5pt]
X^{2}+4X-2X-4X-8=0\\[5pt]
X^{2}-2X-8=0
\end{gather}
\]
Esta é uma Equação do 2.º Grau onde a incógnita é o valor desejado X.
Solução da equação \( X^{2}-2X-8=0 \)
\[
\begin{gather}
\Delta=b^{2}-4ac=(-2)^{2}-4.1.(-8)=4+32=36\\[10pt]
X=\frac{-b\pm \sqrt{\Delta\;}}{2a}=\frac{-2\pm \sqrt{36\;}}{2.1}=\frac{2\pm 6}{2}
\end{gather}
\]
as duas raízes da equação são
\[
\begin{gather}
X=4\;\Omega \qquad \text{ou} \qquad X=-2\;\Omega
\end{gather}
\]
Como não tem sentido resistência com valor negativo, a resistência equivalente vale 4 Ω.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .