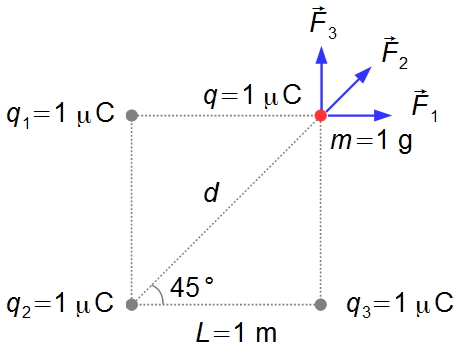
Três cargas elétricas, de 1 μC cada, estão fixas nos vértices de um quadrado de lado 1 m, uma partícula
de carga de 1 μC e massa 1 g é abandonada em repouso no quarto vértice do quadrado, neste momento começa
a sofrer a ação repulsiva das outras cargas. Determinar a aceleração da partícula no momento em que ela é
abandonada.
Dados do problema:
- Valor das cargas: q = 1 μC;
- Massa da carga livre: m = 1 g;
- Distância entre as cargas: L = 1 m;
-
Constante eletrostática do vácuo
\( k_0=9\times 10^9\;\frac{\mathrm{N.m^2}}{\mathrm{C^2}} \).
Esquema do problema:
A força elétrica entre duas cargas está na direção da linha que une estas cargas, então
\( {\vec F}_1 \)
é a força elétrica entre a carga
q e a carga
q1,
\( {\vec F}_2 \)
é a força elétrica entre a carga
q e a carga
q2 e
\( {\vec F}_3 \)
é a força elétrica entre a carga
q e a carga
q3 (Figura 1).
A distância entre as cargas
q e
q2 será a diagonal
d do quadrado,
usando o
Teorema de Pitágoras
\[
\begin{gather}
d^2=L^2+L^2 \\[5pt]
d^2=1^2+1^2 \\[5pt]
d^2=2 \\[5pt]
d=\sqrt{2\;}\;\mathrm m
\end{gather}
\]
Solução:
Em primeiro lugar vamos converter a unidade da massa dada em gramas para quilogramas usado no
Sistema Internacional de Unidades (S.I.).
\[
\begin{gather}
m=1\;\mathrm{\cancel g}\times\frac{1\;\mathrm{kg}}{1000\;\mathrm{\cancel g}}=\frac{1\;\mathrm{kg}}{10^3}=1\times 10^{-3}\;\mathrm{kg}
\end{gather}
\]
Pela
Lei de Coulomb a força elétrica é dada, em módulo, por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{\small E}=k_0\frac{|Q_1||Q_2|}{r^2}} \tag{I}
\end{gather}
\]
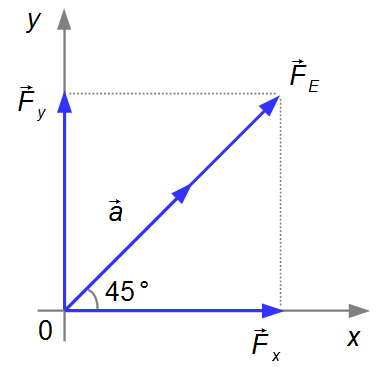
Desenhamos as forças em um sistema de eixos cartesianos e obtemos suas componentes ao longo das
direções
x e
y (Figura 2).
A força
\( {\vec F}_1 \)
só tem componente na direção x, em módulo.
\[
\begin{gather}
F_{1x}=k_0\frac{q\;q_1}{L^2} \\[5pt]
F_{1x}=9\times 10^9\times\frac{1\times 10^{-6}\times 1\times 10^{-6}}{1^2} \\[5pt]
F_{1x}=9\times 10^9\times 1\times 10^{-12} \\[5pt]
F_{1x}=9\times 10^{-3} \tag{II}
\end{gather}
\]
A componente x da força
\( {\vec F}_2 \)
é dada por
\[
\begin{gather}
F_{2x}=F_2\cos 45°
\end{gather}
\]
onde F2 é dado pela equação (I).
Da Trigonometria
\( \cos 45°=\dfrac{\sqrt{2\;}}{2} \)
\[
\begin{gather}
F_{2x}=k_0\frac{q\;q_2}{d^2}\cos 45° \\[5pt]
F_{2x}=9\times 10^9\times\frac{1\times 10^{-6}\times 1\times 10^{-6}}{(\sqrt{2\;})^2}\times\frac{\sqrt{2\;}}{2} \\[5pt]
F_{2x}=9\times 10^9\times\frac{1\times 10^{-12}}{2}\times\frac{\sqrt{2\;}}{2} \\[5pt]
F_{2x}=9\times 10^{-3}\times\frac{\sqrt{2\;}}{4} \tag{III}
\end{gather}
\]
A resultante das forças ao longo da direção x será dada pela soma das equações (II) e (III).
\[
\begin{gather}
F_x=F_{1x}+F_{2x} \\[5pt]
F_x=9\times 10^{-3}+9\times 10^{-3}\times\frac{\sqrt{2\;}}{4} \\[5pt]
F_x=9\times 10^{-3}\times \left(1+\frac{\sqrt{2\;}}{4}\right) \tag{IV}
\end{gather}
\]
A força
\( {\vec F}_3 \)
só tem componente na direção y, em módulo.
\[
\begin{gather}
F_{3y}=k_0\frac{q\;q_3}{L^2} \\[5pt]
F_{3y}=9\times 10^9\times\frac{1\times 10^{-6}\times 1\times 10^{-6}}{1^2} \\[5pt]
F_{3y}=9\times 10^9\times 1\times 10^{-12} \\[5pt]
F_{3y}=9\times 10^{-3} \tag{V}
\end{gather}
\]
A componente y da força
\( {\vec F}_2 \)
é dada por
\[
\begin{gather}
F_{2y}=F_2\operatorname{sen}45°
\end{gather}
\]
onde F2 é dado pela equação (I).
Da Trigonometria
\( \operatorname{sen}45°=\dfrac{\sqrt{2\;}}{2} \)
\[
\begin{gather}
F_{2y}=k_0\frac{q\;q_2}{d^2}\operatorname{sen}45° \\[5pt]
F_{2y}=9\times 10^9\times\frac{1\times 10^{-6}\times 1\times 10^{-6}}{(\sqrt{2\;})^2}\times\frac{\sqrt{2\;}}{2} \\[5pt]
F_{2y}=9\times 10^9\times\frac{1\times 10^{-12}}{2}\times\frac{\sqrt{2\;}}{2} \\[5pt]
F_{2y}=9\times 10^{-3}\times\frac{\sqrt{2\;}}{4} \tag{VI}
\end{gather}
\]
A resultante das forças ao longo da direção y será dada pela soma de (V) e (VI).
\[
\begin{gather}
F_y=F_{3y}+F_{2y} \\[5pt]
F_y=9\times 10^{-3}+9\times 10^{-3}\times\frac{\sqrt{2\;}}{4} \\[5pt]
F_y=9\times 10^{-3}\times\left(1+\frac{\sqrt{2\;}}{4}\right) \tag{VII}
\end{gather}
\]
O módulo da força elétrica resultante FE será obtido usando o Teorema de Pitágoras
usando as equações (IV) e (VII).
\[
\begin{gather}
F_{\small E}^2=F_x^2+F_y^2 \\[5pt]
F_{\small E}^2=\left[9\times 10^{-3}\times\left(1+\frac{\sqrt{2\;}}{4}\right)\right]^2+\left[9\times 10^{-3}\times\left(1+\frac{\sqrt{2\;}}{4}\right)\right]^2 \\[5pt]
F_{\small E}^2=2\times\left[9\times 10^{-3}\times\left(1+\frac{\sqrt{2\;}}{4}\right)\right]^2 \\[5pt]
F_{\small E}=\sqrt{2\times\left[9\times 10^{-3}\times\left(1+\frac{\sqrt{2\;}}{4}\right)\right]^2\;} \\[5pt]
F_{\small E}=9\times 10^{-3}\times\left(1+\frac{\sqrt{2\;}}{4}\right)\times\sqrt{2\;} \\[5pt]
F_{\small E}=9\times 10^{-3}\times\left(\sqrt{2\;}+\frac{\sqrt{2\;}\times\sqrt{2\;}}{4}\right) \\[5pt]
F_{\small E}=9\times 10^{-3}\times\left(\sqrt{2\;}+\frac{2}{4}\right) \\[5pt]
F_{\small E}=9\times 10^{-3}\times\left(\sqrt{2\;}+\frac{1}{2}\right) \\[5pt]
F_{\small E}=1,72\times 10^{-2}\;\mathrm N
\end{gather}
\]
Usando a
2.ª Lei de Newton
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\vec F=m\vec a}
\end{gather}
\]
a única força atuando na carga é a força elétrica
FE, então a aceleração estará na
mesma direção e sentido da força elétrica resultante.
\[
\begin{gather}
F_{\small E}=ma \\[5pt]
a=\frac{F_{\small E}}{m} \\[5pt]
a=\frac{1,72\times 10^{-2}}{1.10^{-3}} \\[5pt]
a=1,72\times 10^{-2}\times 10^3 \\[5pt]
a=1,72\times 10
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{a=17,2\;\mathrm{m/s^2}}
\end{gather}
\]
EN
