Exercício Resolvido de Campo Elétrico

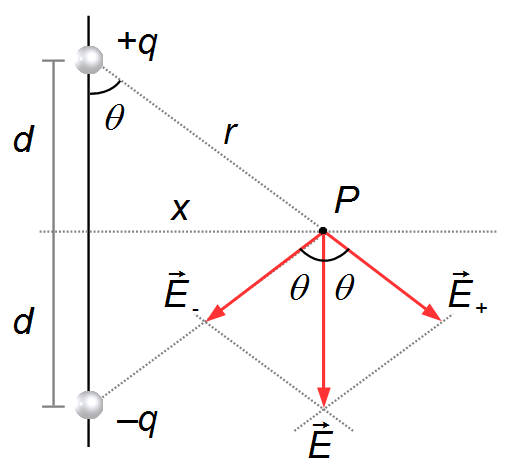
Determine o campo elétrico de um dipolo nos pontos situados na mediatriz do dipolo. Verifique a solução para pontos muito afastados do centro do dipolo.

Construção do vetor campo elétrico resultante

Sobre a mediatriz do dipolo escolhemos um ponto P qualquer onde queremos calcular o campo elétrico. Na direção do segmento de reta que liga a carga +q ao ponto P desenhamos o vetor \( \vec{E}_{\text{+}} \) apontando para “fora” da carga, q>0 (Figura 1).

Figura 1

Na direção do segmento de reta que liga a carga −q ao ponto P desenhamos o vetor \( \vec{E}_{\text{-}} \) apontando para “dentro” da carga, q<0 (Figura 2).

Figura 2

Traçamos pela extremidade do vetor \( \vec{E}_{\text{+}} \) uma reta paralela ao vetor \( \vec{E}_{\text{-}} \) (Figura 3).

Figura 3

Traçamos pela extremidade do vetor \( \vec{E}_{\text{-}} \) uma reta paralela ao vetor \( \vec{E}_{\text{+}} \) (Figura 4).

Figura 4

Do ponto P à intersecção das retas temos o vetor resultante \( \vec{E} \). O ângulo θ que as componentes do campo elétrico, \( \vec{E}_{\text{+}} \) e \( \vec{E}_{\text{-}} \), fazem com o vetor resultante \( \vec{E} \) é o mesmo ângulo que o segmento r faz com o segmento vertical d (Figura 5).

Figura 5

Solução

O módulo do campo elétrico de cada carga é dado por

\[ \begin{gather} \bbox[#99CCFF,10px] {E=k_{0}\frac{q}{r^{2}}} \tag{I} \end{gather} \]

O campo elétrico resultante será dado por

\[ \begin{gather} \vec{E}=\vec{E}_{1}+\vec{E}_{2} \end{gather} \]

como as cargas têm o mesmo valor, em módulo \( E_{1}=E_{2} \)

\[ \begin{gather} E=E_{1}\cos \theta+E_{2}\cos \theta\\[5pt] E=2E_{1}\cos\theta \tag{II} \end{gather} \]

O cosseno de θ é obtido de r e d

\[ \begin{gather} \cos \theta=\frac{d}{r} \tag{III} \end{gather} \]

o segmento r é obtido usando o Teorema de Pitágoras

\[ \begin{gather} r^{2}=d^{2}+x^{2}\\[5pt] r=\sqrt{d^{2}+x^{2}\;} \tag{IV} \end{gather} \]

substituindo a equação (IV) na equação (III)

\[ \begin{gather} \cos \theta=\frac{d}{\sqrt{d^{2}+x^{2}\;}} \tag{V} \end{gather} \]

Substituindo as equações (I) e (V) na equação (II)

\[ \begin{gather} E=2k_{0}\frac{q}{\left(\sqrt{d^{2}+x^{2}\;}\right)^{2}}\frac{d}{\sqrt{d^{2}+x^{2}\;}}\\[5pt] E=2k_{0}\frac{q}{\left(d^{2}+x^{2}\right)}\frac{d}{\left(d^{2}+x^{2}\right)^{\frac{1}{2}}} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {E=\frac{2k_{0}qd}{\left(d^{2}+x^{2}\right)^{\frac{3}{2}}}} \end{gather} \]

Para pontos muito afastados do centro do dipolo temos, x≫d, podemos desprezar o termo em d² no denominador e a solução será

\[ \begin{gather} E=\frac{2k_{0}qd}{x^{{\cancel{2}}\times{\frac{3}{\cancel{2}}}}} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {E=\frac{2k_{0}qd}{x^{3}}} \end{gather} \]

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .