Exercício Resolvido de Movimento Unidimensional
publicidade   

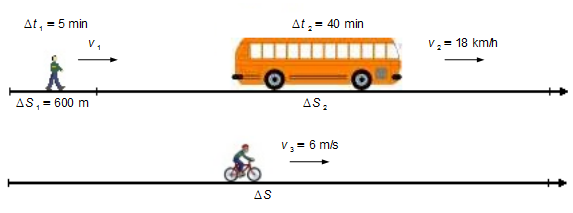
Um operário sai de sua casa e caminha por 600 metros em 5 minutos até o ponto de ônibus, assim que chega ao ponto toma o ônibus e viaja por 40 minutos a uma velocidade constante de 18 quilômetros por hora até a fábrica onde trabalha. Se ele fizesse todo o trajeto de bicicleta, a uma velocidade constante de 6 metros por segundo. Quanto tempo levaria de casa até a fábrica? Dê a resposta em minutos.

Dados do problema:

  • Distância da casa ao ponto de ônibus:    ΔS1 = 600 m;
  • Intervalo de tempo da casa ao ponto de ônibus:    Δt1 = 5 min;
  • Intervalo de tempo do ponto de ônibus à fábrica:    Δt2 = 40 min;
  • Velocidade do ônibus:    vo = 18 km/h;
  • Velocidade da bicicleta:    v3 = 6 m/s.

Esquema do problema:

Adotamos um sistema de referência orientado para a direita (Figura 1)

Figura 1

Solução:

Convertendo os intervalos de tempos dados em minutos para segundos e a velocidade do ônibus dada em quilômetros por hora para metros por segundo usados no Sistema Internacional de Unidades (S.I.)

\[ \begin{gather} \Delta t_1=5\;\mathrm{\cancel{min}}\times\frac{60\;\mathrm s}{1\;\mathrm{\cancel{min}}}=300\;\mathrm s \\[10pt] \Delta t_2=40\;\mathrm{\cancel{min}}\times\frac{60\;\mathrm s}{1\;\mathrm{\cancel{min}}}=2400\;\mathrm s \\[10pt] v_2=18\;\frac{\mathrm{\cancel{km}}}{\mathrm{\cancel h}}\times\frac{1000\;\mathrm m}{1\;\mathrm{\cancel{km}}}\times\frac{1\;\mathrm{\cancel h}}{3600\;\mathrm s}=\frac{18}{3,6}\;\frac{\mathrm m}{\mathrm s}=5\;\mathrm{m/s} \end{gather} \]

O deslocamento total do operário de bicicleta, ΔS, será a soma dos deslocamentos a pé, ΔS1, e de ônibus, ΔS2

\[ \begin{gather} \Delta S=\Delta S_1+\Delta S_2 \tag{I} \end{gather} \]

o deslocamento a pé já é dada no problema ΔS1 = 500 m, como o ônibus se desloca com velocidade constante, sua velocidade coincide com a velocidade média, usando a equação a velocidade média

\[ \begin{gather} \bbox[#99CCFF,10px] {v_m=\frac{\Delta S}{\Delta t}} \end{gather} \]
\[ \begin{gather} v_2=\frac{\Delta S_2}{\Delta t_2} \\[5pt] \Delta S_2=v_2\;\Delta t_2 \\[5pt] \Delta S_2=5\times 2400 \\[5pt] \Delta S_2=12000\;\mathrm m \end{gather} \]

Da equação (I), o deslocamento total será

\[ \begin{gather} \Delta S=600+12000\\[5pt] \Delta S=12600\;\mathrm m \end{gather} \]

como a velocidade da bicicleta é constante também usamos a equação da velocidade média para saber o tempo total do trajeto Δt

\[ \begin{gather} v_3=\frac{\Delta S}{\Delta t} \\[5pt] \Delta t=\frac{\Delta S}{v_3} \\[5pt] \Delta t=\frac{12600}{6} \\[5pt] \Delta t=2100\;\mathrm s \end{gather} \]

convertendo este valor para minutos

\[ \begin{gather} \Delta t=2100\;\mathrm{\cancel s}\times\frac{1\;\mathrm{min}}{60\;\mathrm{\cancel s}}=35\;\mathrm{min} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {\Delta t=35\;\mathrm{min}} \end{gather} \]
publicidade