Exercício Resolvido de Movimento Unidimensional
publicidade   



Durante um nevoeiro um navegador recebe dois sinais expedidos simultaneamente por um posto na costa, um deles através do ar e o outro através da água. Entre as recepções dos dois sons, decorre um intervalo de tempo Δt=5 segundos. Nas condições da experiência, a velocidade do som tem as grandezas, 341 m/s no ar e 1504 m/s na água. Determinar a distância x entre o barco e o posto emissor dos sinais.


Dados do problema:
  • Velocidade do som no ar:    var = 341 m/s;
  • Velocidade do som na água:    vag = 1504 m/s;
  • Intervalo de tempo entre as recepções:    Δt = 5 s.
Esquema do problema:

Como a onda sonora que se propaga pela água tem maior velocidade ela chega antes ao barco. Sendo t o tempo de propagação da onda na água, e t+Δt o tempo de propagação da onda no ar (será a soma do tempo t de propagação na água com o atraso Δt que ela tem por ser mais lenta a propagação).

Figura 1

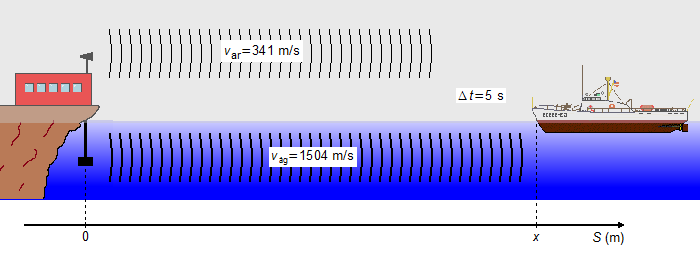
Adotamos um sistema de referência orientado para a direita com origem na posição de emissão do som. A posição inicial das ondas sonoras será S0ar = S0ag = 0, a posição do barco é x, posição final aonde as ondas devem chegar Sar = Sag = x.

Solução

Como as ondas possuem velocidade constante elas estão em Movimento Retilíneo Uniforme (M.R.U.) dado por
\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+v t} \tag{I} \end{gather} \]
Aplicando a equação (I) para a onda que se propaga pela água
\[ \begin{gather} S_{ag}=S_{0ag}+v_{ag}t\\[5pt] x=0+1504t\\[5pt] x=1504t \tag{II} \end{gather} \]
Aplicando a equação (I) para a onda que se propaga pelo ar
\[ \begin{gather} S_{ar}=S_{0ar}+v_{ar}t\\[5pt] x=0+341(t+\Delta t)\\[5pt] x=341(t+5) \tag{III} \end{gather} \]
Da equação (II) podemos isolar o valor de t
\[ \begin{gather} t=\frac{x}{1504} \tag{IV} \end{gather} \]
substituindo a expressão (IV) na equação (III)
\[ \begin{gather} x=341\left(\frac{x}{1504}+5\right)\\[5pt] x=\frac{341}{1504}x+341\times 5\\[5pt] x=\frac{341}{1504}x+1705\\[5pt] x-\frac{341}{1504}x=1705 \end{gather} \]
multiplicando ambos os lados da igualdade por 1504
\[ \begin{gather} \qquad\qquad\qquad x-\frac{341}{1504}x=1705 \qquad (\times 1504)\\[5pt] 1504 x-\cancel{1504}\times\frac{341}{\cancel{1504}}x=1705\times 1504\\[5pt] 1163x=2564320\\[5pt] x=\frac{2564320}{1163} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {x\approx 2205\;\mathrm m} \end{gather} \]
publicidade   

Licença Creative Commons
Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .