Solved Problem on Kinematics
advertisement
A particle is on a plane xy, initially at rest in the position x0 on the positive x-axis. It begins to move with constant velocities vx, in the direction of origin, and vy in the direction of the positive y-axis. Determine after how long the particle will be at the minimum distance of the origin and, what is this minimum distance.
Problem data:
- Initial position of the particle: x0;
- Speed of the particle in direction x: vx;
- Speed of the particle in direction y: vy.
As the components of the speed are constants the trajectory will be a straight line (Figure 1-A).

Throughout the trajectory, the particle passes successively by points P0, P1, P2, PP, P3, and so on, located by the vectors r0, r1, r2, rP, r3, respectively. The point of minimum distance to the origin will be the point PP, where the vector rP is perpendicular to a vector in the trajectory (Figure 1-B).
Solution
The position vector rP is written as
\[
\begin{gather}
{\mathbf{r}}_{P}={\mathbf{r}}_{0}+\mathbf{v} t \tag{I}
\end{gather}
\]
which is the vector equation for a body in motion with constant velocity, the initial position vector
r0 only has a component along the x direction,
\( {\mathbf{r}}_{0}={x}_{0}\;\mathbf{i} \),
the vector along the trajectory has components in the x and y directions,
\( \mathbf{v}\;t=-v_{x}t\;\mathbf{i}+v_{y}t\;\mathbf{j} \)
(Figure 2-A) so the expression (I) can be written as
\[
\begin{gather}
{\mathbf{r}}_{P}={x}_{0}\;\mathbf{i}+\left(-{v}_{x}t\;\mathbf{i}+{v}_{y}t\;\mathbf{j}\right)\\
{\mathbf{r}}_{P}={x}_{0}\;\mathbf{i}-{v}_{x}t\;\mathbf{i}+{v}_{y}t\;\mathbf{j}\\
{\mathbf{r}}_{P}=\left({x}_{0}-{v}_{x}t\right)\;\mathbf{i}+{v}_{y}t\;\mathbf{j} \tag{II}
\end{gather}
\]
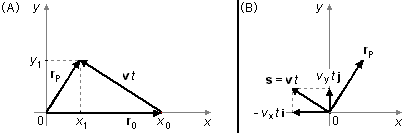
The displacement vector \( \mathbf{s}=-v_{x}t\;\mathbf{i}+v_{y}t\;\mathbf{j} \) is parallel to the trajectory (Figure 2-B) so that the vectors rP and s are perpendicular to each other, we must have the condition that the dot product between them is zero
\[
\begin{gather}
{\mathbf{r}}_{P}\cdot{\mathbf{s}}=0\\[5pt]
\left[\left(x_{0}-v_{x}t\right)\;\mathbf{i}+v_{y}t\;\mathbf{j}\right]\cdot\left[-v_{x}t\;\mathbf{i}+v_{y}t\;\mathbf{j}\right]=0\\[5pt]
\left(x_{0}-v_{x}t\right)\left(-v_{x}t\right)\underbrace{\mathbf{i}\cdot\mathbf{i}}_{1}+v_{y}t\;v_{y}t\underbrace{\mathbf{j}\cdot\mathbf{j}}_{1}=0\\[5pt]
-x_{0}v_{x}t+v_{x}^{2}t^{2}+v_{y}^{2}t^{2}=0\\[5pt]
t\left(-x_{0}v_{x}+v_{x}^{2}t+v_{y}^{2}t\right)=0
\end{gather}
\]
from this expression, we have two values for the time
\[
\begin{gather}
t=0\\[5pt]
\text{or}\\[5pt]
-x_{0}v_{x}+v_{x}^{2}t+v_{y}^{2}t=0\\
t\left(v_{x}^{2}+v_{y}^{2}\right)=x_{0}v_{x}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{t=\frac{x_{0}v_{x}}{v_{x}^{2}+v_{y}^{2}}}
\]
Substituting this value in the expression (II), we have the position vector that gives the minimum distance
of the particle to the origin
\[
{\mathbf{r}}_{P}=\left({x}_{0}-{v}_{x}\frac{x_{0}v_{x}}{v_{x}^{2}+v_{y}^{2}}\right)\;\mathbf{i}+{v}_{y}t\;\mathbf{j}
\]
the magnitude is
\[
\begin{gather}
r_{P}=\sqrt{\left(x_{0}-v_{x}\frac{x_{0}v_{x}}{v_{x}^{2}+v_{y}^{2}}\right)^{2}+\left(v_{y}\frac{x_{0}v_{x}}{v_{x}^{2}+v_{y}^{2}}\right)^{2}\;}\\[5pt]
r_{P}=\sqrt{\left(\frac{x_{0}(v_{x}^{2}+v_{y}^{2})-x_{0}v_{x}^{2}}{v_{x}^{2}+v_{y}^{2}}\right)^{2}+\left(\frac{x_{0}v_{x}v_{y}}{v_{x}^{2}+v_{y}^{2}}\right)^{2}\;}\\[5pt]
r_{P}=\sqrt{\;\left(\frac{{x}_{0}v_{y}^{2}}{v_{x}^{2}+v_{y}^{2}}\right)^{2}+\left(\frac{x_{0}v_{x}{v}_{y}}{v_{x}^{2}+v_{y}^{2}}\right)^{2}\;}\\[5pt]
r_{P}=\sqrt{\frac{{x}_{0}^{2}v_{y}^{4}+x_{0}^{2}v_{x}^{2}v_{y}^{2}}{(v_{x}^{2}+v_{y}^{2})^{2}}\;}\\[5pt]
r_{P}=\sqrt{\frac{{x}_{0}^{2}v_{y}^{2}(v_{y}^{2}+v_{y}^{2})}{(v_{x}^{2}+v_{y}^{2})^{2}}\;}\\[5pt]
r_{P}=\sqrt{\frac{{x}_{0}^{2}v_{y}^{2}}{v_{x}^{2}+v_{y}^{2}}\;}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{r_{P}=\frac{{x}_{0}v_{y}}{\sqrt{v_{x}^{2}+v_{y}^{2}\;}}}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .