Solved Problem on Inertia
Português
English
advertisement
Derive the Parallel Axis Theorem.
Problem diagram:
In Figure 1, dm is an element of mass of the body, r is the distance from the mass element
to the axis perpendicular to the center of mass of the body, s is the distance from the mass
element to an axis parallel to the axis passing through the center of mass and d is the distance
between the two axes.
Solution
In Figure 2, we have a top view of the body, the axis through the center of mass and the parallel axis
are perpendicular to the screen. In the figure, x and y locate the mass element dm
relative to the center of mass, and xp and yp locate the parallel
axis relative to the center of mass.
The moment of inertia relative to the axis passing through the center of mass is given by
The moment of inertia relative to the axis passing through the center of mass is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{I_{CM}=\int r^{2}\;dm} \tag{I}
\end{gather}
\]
from Figure 2, using the Pythagorean Theorem
\[
\begin{gather}
r^{2}=x^{2}+y^{2} \tag{II}
\end{gather}
\]
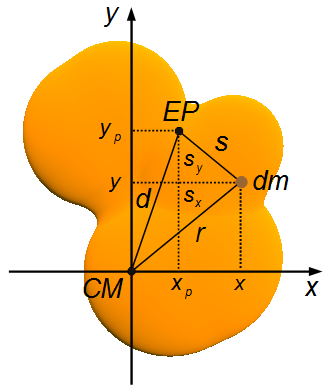
Figure 2
substituting the expresssion (II) into expression (I)
\[
\begin{gather}
I_{CM}=\int \left(x^{2}+y^{2}\right)\;dm \tag{III}
\end{gather}
\]
The moment of inertia relative to an axis parallel to the axis passing through the center of mass is given by
\[
\begin{gather}
I=\int s^{2}\;dm \tag{IV}
\end{gather}
\]
from Figure 2, we can write sx and sy
\[
\begin{gather}
s_{x}=x-x_{p} \tag{V-a}
\end{gather}
\]
\[
\begin{gather}
s_{y}=y_{p}-y \tag{V-b}
\end{gather}
\]
using the Pythagorean Theorem
\[
\begin{gather}
s^{2}=s_{x}^{2}+s_{y}^{2}\\
s^{2}=(x-x_{p})^{2}+(y_{p}-y)^{2} \tag{VI}
\end{gather}
\]
substituting the expression (VI) into expression (IV)
\[
I=\int \left[(x-x_{p})^{2}+(y_{p}-y)^{2}\right]\;dm
\]
Expanding the binomial in the integral
\( (a-b)^{2}=a^{2}-2 ab+b^{2} \)
\[
\begin{gather}
I=\int\left[x^{2}-2 xx_{p}+x_{p}^{2}+y_{p}^{2}-2 yy_{p}+y^{2}\right]\;dm\\
I=\int\left[\left(x^{2}+y^{2}\right)-2 xx_{p}-2 yy_{p}+\left(x_{p}^{2}+y_{p}^{2}\right)\right]\;dm
\end{gather}
\]
the integral of the sum of functions is the sum of the integrals
\[
I=\int \left(x^{2}+y^{2}\right)\;dm-\int2 xx_{p}\;dm-\int 2 yy_{p}\;dm+\int\left(x_{p}^{2}+y_{p}^{2}\right)\;dm
\]
The first integral represents the moment of inertia relative to the axis that passes through the center of
mass given by the expression (III). In the second and third integrals, the terms 2xp and
2yp are constants and in the fourth integral,
xp2+yp2 is constant, it represents the distance
between the axes, moving these terms out of the integral
\[
\begin{gather}
I=I_{CM}-2x_{p}\int x\;dm-2y_{p}\int y\;dm+\left(x_{p}^{2}+y_{p}^{2}\right)\int \;dm \tag{VII}
\end{gather}
\]
In the integrals
\( \int x\;dm=0 \)
and
\( \int y\;dm=0 \),
all elements of mass multiplied by distance and added are equal to zero, relative to the center of
mass of the body.
Note:
\( \int r\;dm=0 \):
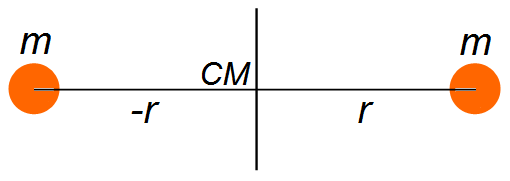
Figure 3
Figure 4
The distances of the masses to the center of mass are different (rm > rM), but the masses are also different (m < M), this makes the products rmm e rMM equal and the adds zero.
Another system with three different masses with values m1, m2, and m3 and placed at distances r1 r2 and, r3 from the center of mass of the system. We choose a frame of reference in the center of mass. Decomposing the position vectors in x and y directions, and calculating the product of the masses by the distance to the center of mass in the x and y directions and adding the results (figures 5-A and 5-B)
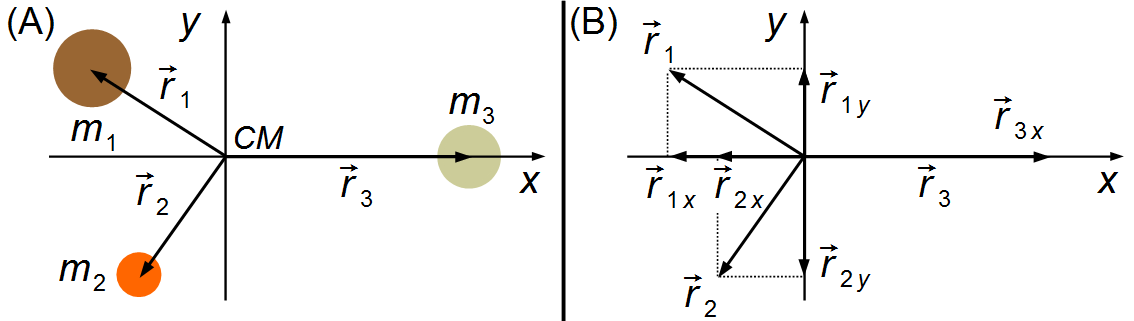Figure 5
The distances from the masses to the center of mass are different, but the masses are also different, this makes rimi products in the x and y directions equal and adds zero.
Figure 6
We have a system with two equal masses m and placed the same distance r from the center
of mass of the system. We choose a frame of reference in the center of mass. Calculating the product
of the masses by the distance to the center of mass and adding the results (Figure 3)
Figure 3
\[
\sum_{i}r_{i}m_{1}=rm+(-r)m=rm-rm=0
\]
We have another system with two different masses with m and M and placed at distances
rm and rM from the center of mass of the system. We choose a frame
of reference in the center of mass. Calculating the product of the masses by the distance to the
center of mass and adding the results (Figure 4)
Figure 4
\[
\sum_{i}r_{i}m_{1}=r_{m}m+(-r_{M})M=r_{m}m-r_{M}M=0
\]
The distances of the masses to the center of mass are different (rm > rM), but the masses are also different (m < M), this makes the products rmm e rMM equal and the adds zero.
Another system with three different masses with values m1, m2, and m3 and placed at distances r1 r2 and, r3 from the center of mass of the system. We choose a frame of reference in the center of mass. Decomposing the position vectors in x and y directions, and calculating the product of the masses by the distance to the center of mass in the x and y directions and adding the results (figures 5-A and 5-B)
\[
\begin{split}
\sum_{i}r_{xi}m_{i} &=-r_{1x}m_{1}+(-r_{2x})m_{2}+r_{3x}m_{3}=\\
&=-r_{1x}m_{1}-r_{2x}m_{2}+r_{3x}m_{3}=0
\end{split}
\]
\[
\begin{split}
\sum_{i}r_{yi}m_{i} &=r_{1y}m_{1}+(-r_{2y})m_{2}+0.m_{3}=\\
&=r_{1y}m_{1}-r_{2y}m_{2}+0=0
\end{split}
\]
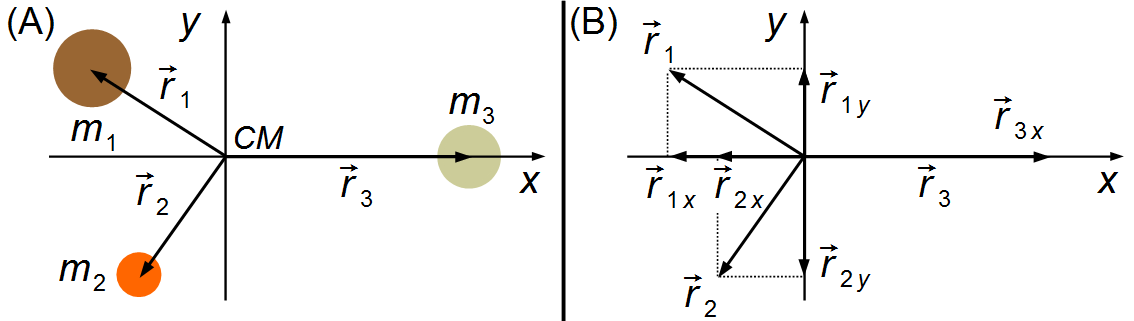
The distances from the masses to the center of mass are different, but the masses are also different, this makes rimi products in the x and y directions equal and adds zero.
For a rigid body of mass M, we consider mass element dm given by the position vector
r relative to the center of mass of the system. We choose a frame of reference in the center of
mass. As we have a continuous mass distribution we change from the sum to integral. Integration on all
mass elements will be zero (Figure 6)
\[
\int r\;dm=0
\]
Figure 6
The integral \( \int_{0}^{M}dm=M \), represents the total mass of the body. In the Figure 2 using the Pythagorean Theorem
\[
\begin{gather}
d^{2}=x_{p}^{2}+y_{p}^{2} \tag{VIII}
\end{gather}
\]
Substituting the expression (VIII) into expression (VII), the moment of inertia of the body relative to an
axis parallel to the axis passing through the center of mass will be
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{I=I_{CM}+Md^{2}} \tag{Q.E.D.}
\end{gather}
\]
Observação: Q.E.D é a abreviação da expressão em latim Quod Erat Demonstrandum que
significa Como Queríamos Demonstrar.
advertisement
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .