Solved Problem on Optical Instruments

In a compound microscope, the focal length of the objective is 2 mm, and that of the ocular is 10 mm. The length of the tube that supports the lenses is 18 cm. The final image of the system is formed at 50 cm from the eyepiece. Determine:
a) The magnification of the objective and eyepiece;
b) The magnification of the microscope;

Problem data:

Objective focal length: f₁ = 2 mm;
Eyepiece focal length: f₂ = 10 mm;
Distance from the image to the eyepiece: p'₂ = −50 cm;
Distance between lenses: d = 18 cm.

Image construction:

Using the rule, all rays of light incident at the center of the lens continue in a straight line, and we see a ray of light that passes through the optical center of the objective O₁

Figure 1

Using the rule, all rays of light parallel to the principal axis pass through the focal point F', and we have a second parallel ray of light that comes out through the focus F'₁. From the crossing of the two rays, we have a point where the image i₁ of the objective is formed (Figure 2).

Figure 2

Image i₁ from the objective becomes object o₂ for the eyepiece, \( i_{1}\equiv o_{2} \). Again, a ray passing through the optical center, now from the ocular, O₂, does not deviate (Figure 3).

Figure 3

Again, a parallel ray passes through the image focus, this time from the eyepiece F'₂ (Figure 4).

Figure 4

These two rays do not determine an image on the observer's side. To determine the image it is necessary to extend these rays to the side of the object o₂ from their crossing, and we have the enlarged image i₂ (Figure 5).

Figure 5

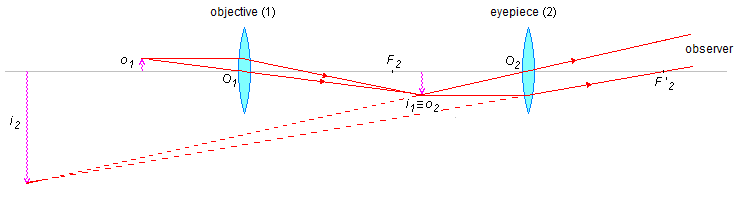
Problem diagram:

Figure 6

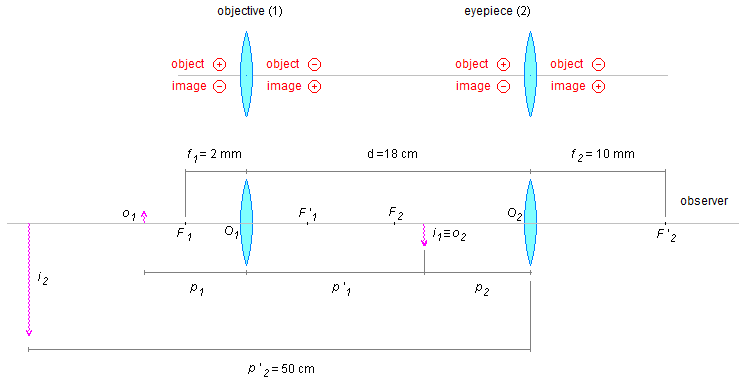
Using the sign convention, on the incident light side, we have the positive abscissa for the real object, p > 0, and negative for the virtual image, p' < 0, and on the opposite side, we have the negative abscissa of the virtual object, p < 0, and positive for the real image, p' > 0.
Image i₁ has a positive abscissa, as it is behind the objective lens p'₁ > 0, real image, it is also an object for the eyepiece, as it is in front of the lens it has a positive abscissa, p₂ > 0, real object, image i₂ is in front of the eyepiece, so it is a virtual image and has a negative abscissa p'₂ < 0.

Solution

a) First, let us convert all units to centimeters (cm)

\[ \begin{gather} f_{1}=2\;\text{mm}=2\times 10^{-1}\;\text{cm}=0.2\;\text{cm}\\[10pt] f_{2}=10\;\text{mm}=10\times 10^{-1}\;\text{cm}=1\;\text{cm} \end{gather} \]

To find p₂, we use the Thin Lens Equation

\[ \begin{gather} \bbox[#99CCFF,10px] {\frac{1}{f}=\frac{1}{p}+\frac{1}{p'}} \end{gather} \]

applying to the second lens (eyepiece)

\[ \begin{gather} \frac{1}{f_{2}}=\frac{1}{p_{2}}+\frac{1}{p'_{2}}\\[5pt] \frac{1}{p_{2}}=\frac{1}{f_{2}}-\frac{1}{p'_{2}}\\[5pt] \frac{1}{p_{2}}=\frac{1}{1}-\frac{1}{(-50)}\\[5pt] \frac{1}{p_{2}}=1+\frac{1}{50} \end{gather} \]

multiplying and dividing by 50, the first term on the right-hand side of the equation

\[ \begin{gather} \frac{1}{p_{2}}=\frac{50}{50}\times 1+\frac{1}{50}\\[5pt] \frac{1}{p_{2}}=\frac{50+1}{50}\\[5pt] \frac{1}{p_{2}}=\frac{51}{50}\\[5pt] p_{2}=\frac{50}{51} \tag{I}\\[5pt] p_{2}=0.98\;\text{cm} \end{gather} \]

the eyepiece magnification M_e is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {M_{e}=\frac{i_{2}}{o_{2}}=-{\frac{p'_{2}}{p_{2}}}} \end{gather} \]

using for p₂ the value given by (I)

\[ \begin{gather} M_{e}=-{\frac{(-50)}{\dfrac{50}{51}}}\\[5pt] M_{e}=\cancel{50}.\frac{51}{\cancel{50}} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {M_{e}=51} \end{gather} \]

The length of the tube will be the sum of the distance from the objective to the image, \( i_{1}\equiv o_{2} \), p'₁, with the distance from the object \( i_{1}\equiv o_{2} \) to the ocular, p₂ (Figure 6).

\[ \begin{gather} d=p'_{1}+p_{2}\\[5pt] 18=p'_{1}+0.98\\[5pt] p'_{1}=18-0.98\\[5pt] p'_{1}=17.02\;\text{cm} \end{gather} \]

Applying the Thin Lens Equation, we find the distance of object i₁ to the objective

\[ \begin{gather} \frac{1}{f_{1}}=\frac{1}{p_{1}}+\frac{1}{p'_{1}}\\[5pt] \frac{1}{p_{1}}=\frac{1}{f_{1}}-\frac{1}{p'_{1}}\\[5pt] \frac{1}{p_{1}}=\frac{1}{0.2}-\frac{1}{17.02} \end{gather} \]

writing \( 0.2=\frac{2}{10} \) and \( 17.02=\frac{1702}{100} \)

\[ \begin{gather} \frac{1}{p_{1}}=\frac{1}{\dfrac{2}{10}}+\frac{1}{\dfrac{1702}{100}}\\[5pt] \frac{1}{p_{1}}=\frac{10}{2}+\frac{100}{1702} \end{gather} \]

multiplying and dividing by 851, the first term on the right-hand side of the equation

\[ \begin{gather} \frac{1}{p_{1}}=\frac{8510-100}{1702}\\[5pt] \frac{1}{p_{1}}=\frac{8410}{1702}\\[5pt] p_{1}=\frac{1702}{8410} \tag{II}\\[5pt] p_{1}\approx 0.2\;\text{cm} \end{gather} \]

the magnification of objective M_o is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {M_{o}=\frac{i_{1}}{o_{1}}=-{\frac{p'_{1}}{p_{1}}}} \end{gather} \]

using for p₁ the value given by (II)

\[ \begin{gather} M_{o}=-{\frac{\dfrac{1702}{100}}{\dfrac{1702}{8410}}}\\[5pt] M_{o}=-{\frac{\cancel{1702}}{100}\times\frac{8410}{\cancel{1702}}}\\[5pt] M_{o}=-{\frac{8410}{100}} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {M_{o}=-84.1} \end{gather} \]

b) The magnification of the microscope will be

\[ \begin{gather} M=M_{o}.M_{e}\\[5pt] M=(-84.1)\times 51 \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {M=-4289.1} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .