Solved Problem on Kepler's Laws and Gravitation

In the film 2001: A Space Odyssey (1968 directed by Stanley Kubrick) the spacecraft Discovery One has a section formed by a centrifuge that rotates in order to produce artificial gravity similar to the gravity of the Moon.

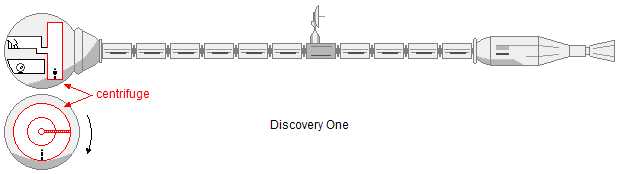
Assuming that an astronaut has an average height of 1.70 m and that the centrifuge has a diameter of 11.6 m and rotates at a frequency of 5 rpm, check if it is possible to build such a device.

Problem data:

Centrifuge diameter: D = 11.6 m;
Centrifuge rotation frequency: f = 5 rpm;
Astronaut height: h = 1.70 m.

Problem diagram:

Since the centrifuge has a diameter of 11.6 m, its radius is

\[ \begin{gather} R=\frac{D}{2}\\ R=\frac{11.6}{2}\\ R=5.8\;\text{m} \end{gather} \]

this is the distance from the feet of the astronaut to the center of the centrifuge.
The head of the astronaut is at a distance d from the center equal to

\[ \begin{gather} d=R-h\\ d=5.8-1.7\\ d=4.1\;\text{m} \end{gather} \]

With these data, we can calculate the artificial gravity generated by rotating the centrifuge at the height of the feet of the astronaut, \( \vec{g}_{f} \), and head, \( \vec{g}_{h} \) (Figure 1).

Figure 1

Solution

First, we must convert the given frequency in revolutions per minute (rpm) to hertz (Hz) used in the International System of Units (SI)

\[ \begin{gather} f=5\;\text{rpm}=5\;\frac{\text{rotations}}{1\;\cancel{\text{min}}}\times\frac{1\;\cancel{\text{min}}}{60\;\text{s}}=\frac{5}{60}\;\frac{\text{rotations}}{\text{s}}=\frac{1}{12}\;\frac{\text{rotations}}{\text{s}}=\frac{1}{12}\;\text{Hz} \end{gather} \]

Forces acting on the astronaut (Figure 2):

\( {\vec{F}}_{CP} \): centripetal force acting on the astronaut due to the rotation of the centrifuge;
\( {\vec{F}}_{CG} \): centrifugal force that acts on the astronaut, keeps the astronaut on the floor of the centrifuge producing artificial gravity.

Note: The centrifugal force, \( {\vec{F}}_{CG} \), is not the reaction of the centripetal force, \( {\vec{F}}_{CP} \), by Newton's Third Law, action and reaction forces are on different bodies, and in this case, the two forces are applied to the astronaut.

Figure 2

The artificial gravity produced by the rotation is given by the centrifugal force and is equal to the centripetal force, in magnitude, given by

\[ \begin{gather} F_{CG}=F_{CP}=m\frac{v^{2}}{r} \end{gather} \]

Applying Newton's Second Law

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec{F}=m\vec{a}} \end{gather} \]

the resultant force that produces artificial gravity is the centrifugal force, so we write its magnitude

\[ \begin{gather} m\frac{v^{2}}{r}=ma\\ a=\frac{v^{2}}{r} \tag{I} \end{gather} \]

the tangential speed is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {v=\omega r} \tag{II} \end{gather} \]

substituting expression (II) into expression (I)

\[ \begin{gather} a=\frac{(\omega r)^{2}}{r}\\ a=\frac{\omega^{2}r^{2}}{r}\\ a=\omega ^{2}r \tag{III} \end{gather} \]

The angular speed is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {\omega =2\pi f} \tag{IV} \end{gather} \]

substituting expression (IV) into expression (III)

\[ \begin{gather} a=(2\pi f)^{2}r\\ a=4\pi^{2}f^{2}r \tag{V} \end{gather} \]

Using the given frequency, taking π = 3.14 and using r = R = 5.8 m, we have the acceleration produced at the height of the feet of the astronaut, a = g_f

\[ \begin{gather} g_{f}=4\times 3.14^{2}\times \left(\frac{1}{12}\right)^{2}\times 5.8\\ g_{f}=4\times 9.86\times \frac{1}{144}\times 5.8\\ g_{f}=1.59\;\text{m/s}^{2} \end{gather} \]

Using r = d = 4.1 m, we have the acceleration generated at the height of the head of the astronaut, a = g_h

\[ \begin{gather} g_{h}=4\times 3.14^{2}\left(\frac{1}{12}\right)^{2}\times 4.1\\ g_{h}=4\times 9.86.\frac{1}{144}\times 4.1\\ g_{h}=1.12\;\text{m/s}^{2} \end{gather} \]

The difference in values between the acceleration due to gravity in the head and feet is very large, this would make it difficult for astronauts to walk, blood circulation could also be compromised, with a lack of blood in the head, which would be attracted to the feet, causing vertigo. and fainting of the astronauts. Therefore, it would not be possible to build a centrifuge with these dimensions.

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .