Solved Problem on Dynamics

Two blocks, with masses m_A and m_B, are released from the rest on very long inclined planes. Block A is on a plane that makes an angle α with the horizontal, and block B is on a plane with an angle β. Assume the acceleration due to gravity is equal to g, and there is no friction between the blocks and the inclined planes. Determine the ratio of distances traveled by the blocks until both have the same speed.

Problem data:

Mass of block A: m_A;
Mass of block B: m_B;
Initial speed of block A: v_0A = 0;
Initial speed of block B: v_0B = 0;
Angle of plane A: α;
Angle of plane B: β;
Acceleration due to gravity: g;

Problem diagram:

For each plane, we choose a frame of reference pointed in the downward direction of the inclined plane and with the x-axis parallel to the plane (Figure 1).

Figura 1

Drawing free-bodies diagrams, we have the forces that act in each of them.
Block A (Figure 2):

\( {\vec F}_{gA} \): gravitational force on block A;
\( {\vec N}_{A} \): normal reaction force of plane on block A.

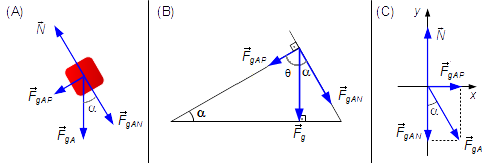
The gravitational force \( {\vec F}_{gA} \) can be decomposed into two components, a component parallel to the x-axis \( {\vec F}_{gAP} \) and the other normal or perpendicular component \( {\vec F}_{gAN} \) (Figure 2-A).

Figure 2

In the triangle on the left in Figure 2-B, the gravitational force \( {\vec F}_{gA} \) is perpendicular to the horizontal plane, makes a 90° angle, the angle between the inclined plane and the horizontal plane is equal to α, as the sum of interior angles of a triangle equals to 180°, the angle θ between the gravitational force and the parallel component \( {\vec F}_{gAP} \) will be

\[ \alpha +\theta +90°=180°\Rightarrow \theta=180°-90°-\alpha\Rightarrow \theta=90°-\alpha \]

In the triangle on the right, the components of gravitational force in the x and y directions are perpendicular to each other, the angle between the gravitational force and \( {\vec F}_{gA} \) the component of gravitational force in the y direction \( {\vec F}_{gAN} \), will be

\[ 90°-\theta \Rightarrow 90°-(90°-\alpha)\Rightarrow 90°-90°+\alpha \Rightarrow \alpha \]

Drawing the forces in a coordinate system xy (Figure 2 -C) and apply Newton's Second Law
Block B (Figure 3):

\( {\vec F}_{gB} \): gravitational force on block B;
\( {\vec N}_{B} \): normal reaction force of plane on block B.

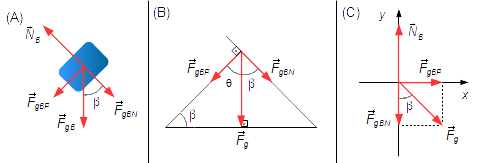
The gravitational force \( {\vec F}_{gB} \) can be decomposed into two components, a component parallel to the x-axis \( {\vec F}_{gBP} \) and the normal or perpendicular \( {\vec F}_{gBN} \) (Figure 3-A).

Figure 3

In the triangle on the left in Figure 3-B, the gravitational force \( {\vec F}_{gB} \) is perpendicular to the horizontal plane, makes a 90° angle, the angle between the inclined plane and the horizontal plane is equal to β, as the sum of interior angles of a triangle equals to 180°, the angle θ between the gravitational force and the parallel component \( {\vec F}_{gBP} \), will be

\[ \beta +\theta +90°=180°\Rightarrow \theta=180°-90°-\beta\Rightarrow \theta=90°-\beta \]

In the triangle to the right to components of gravitational force in x and y directions are perpendicular to each other, the angle between the gravitational force \( {\vec F}_{gB} \) and the component of gravitational force in the y direction \( {\vec F}_{gBN} \), will be

\[ 90°-\theta \Rightarrow 90°-(90°-\beta)\Rightarrow 90°-90°+\beta \Rightarrow \beta \]

Drawing the forces in coordinate system xy (Figure 3-C), we can apply Newton's Second Law

Solution

Using Newton's Second Law

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec{F}=m\vec{a}} \tag{I} \end{gather} \]

Block A:

Direction x:

\[ \begin{gather} F_{gAP}=m_{A}a_{A} \tag{II} \end{gather} \]

the parallel component of the gravitational force is given by

\[ \begin{gather} F_{gAP}=F_{gA}\sin \alpha \tag{III} \end{gather} \]

the gravitational force is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {F_{g}=mg} \tag{IV} \end{gather} \]

for block A

\[ \begin{gather} F_{gA}=m_{A}g \tag{V} \end{gather} \]

substituting the expression (V) into expression (III)

\[ \begin{gather} F_{gAP}=m_{A}g\sin \alpha \tag{VI} \end{gather} \]

substituting the expression (VI) into expression (II)

\[ \begin{gather} \cancel{m_{A}}g\sin \alpha =\cancel{m_{A}}a_{A}\\[5pt] a_{A}=g\sin \alpha \end{gather} \]

Applying the equation of velocity as a function of displacement, we calculate the distance traveled, L_A, by the block

\[ \begin{gather} \bbox[#99CCFF,10px] {v^{2}=v_{0}^{2}+2a\Delta S} \tag{VII} \end{gather} \]

\[ \begin{gather} v_{A}^{2}=v_{0A}^{2}+2a_{A}\Delta S_{A}\\[5pt] v_{A}^{2}=0^{2}+2g\sin \alpha L_{A}\\[5pt] L_{A}=\frac{v_{A}^{2}}{2g\sin \alpha} \tag{VIII} \end{gather} \]

Block B:

Direction x:

\[ \begin{gather} F_{gBP}=m_{B}a_{B} \tag{IX} \end{gather} \]

the parallel component of the gravitational is given by

\[ \begin{gather} F_{gBP}=F_{gB}\sin \beta \tag{X} \end{gather} \]

for block B, using expression (IV) for gravitational force

\[ \begin{gather} F_{gB}=m_{B}g \tag{XI} \end{gather} \]

substituting the expression (XI) into expression (X)

\[ \begin{gather} F_{gBP}=m_{B}g\sin \beta \tag{XII} \end{gather} \]

substituting the expression (XII) into expression (IX)

\[ \begin{gather} \cancel{m_{B}}g\sin \beta =\cancel{m_{B}}a_{B}\\[5pt] a_{B}=g\sin \beta \end{gather} \]

Applying the expression (VII) to block B, the distance traveled L_B will be

\[ \begin{gather} v_{B}^{2}=v_{0B}^{2}+2a_{B}\Delta S_{B}\\[5pt] v_{B}^{2}=0^{2}+2g\sin \beta L_{B}\\[5pt] L_{B}=\frac{v_{B}^{2}}{2g\sin \beta } \tag{XIII} \end{gather} \]

Applying the condition given in the problem, from the speeds of the two blocks should be equal, we have v_A = v_B = v. The problem says that planes are very long, this means that the blocks can descend until their speeds are equal before reaching the end of the plane.
Dividing the expression (VIII) by (XIII)

\[ \begin{gather} \frac{L_{A}}{L_{B}}=\frac{\dfrac{\cancel{v^{2}}}{\cancel{2}\cancel{g}\sin \alpha}}{\dfrac{\cancel{v^{2}}}{\cancel{2}\cancel{g}\sin \beta }} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {\frac{L_{A}}{L_{B}}=\frac{\operatorname{sen\beta}}{\sin \alpha}} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .