Solved Problem on Dynamics
advertisement
An Atwood machine consists of a block A, with mass equal to 100 kg, and a block B, with
mass equal to 300 kg with the shape of a cube of edge equal to 0.60 m immersed in a container with water.
The blocks are attached by an inextensible rope and negligible mass that passes through a frictionless
pulley and negligible mass. Determine:
a) Acceleration of the system;
b) The tension force on the rope that connects the masses.
Assume the density of water is equal to 1000 kg/m3, and the acceleration due to gravity is equal to 10 m/s2.
a) Acceleration of the system;
b) The tension force on the rope that connects the masses.
Assume the density of water is equal to 1000 kg/m3, and the acceleration due to gravity is equal to 10 m/s2.

Problem data:
- Mass of block A: mA = 100 kg;
- Mass of block B: mB = 300 kg;
- Length of edge of block B: b = 0,60 m;
- Water density: ρ = 1000 kg/m3;
- Acceleration due to gravity: g = 10 m/s2.
As the mass of block B is greater than the mass of block A, we will assume a frame of
reference positive in the direction of block B is descending, the same direction of the
acceleration due to gravity, and with block A rising.
The cord and pulley have no mass and friction, the acceleration is the same for the whole system. The rope only transmits the tension force between the blocks (Figure 1).
The cord and pulley have no mass and friction, the acceleration is the same for the whole system. The rope only transmits the tension force between the blocks (Figure 1).

Solution
a) Drawing free-bodies diagrams, we have the forces that act in each of them, and we apply Newton's Second Law
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\vec{F}=m\vec{a}} \tag{I}
\end{gather}
\]
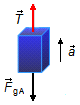
Body A:
- \( \vec{T} \): tension force on the rope;
- \( {\vec F}_{gA} \): gravitational force on block A.
\[
\begin{gather}
T-F_{gA}=m_{A}a \tag{II}
\end{gather}
\]
The gravitational force is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{g}=mg} \tag{III}
\end{gather}
\]
substituting the expression (III) to block A, into expression (II)
\[
\begin{gather}
T-m_{A}g=m_{A}a \tag{IV}
\end{gather}
\]
Body B:
- \( \vec{T} \): tension force on the rope;
- \( \vec{B} \): buoyant force;
- \( {\vec F}_{gB} \): gravitational force on block B.
\[
\begin{gather}
F_{gB}-T-B=m_{B}a \tag{V}
\end{gather}
\]

The buoyant force is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{B=\rho gV} \tag{VI}
\end{gather}
\]
the volume of a cube is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{V=b^{3}} \tag{VII}
\end{gather}
\]
substituting the expression (VII) into expression (VI)
\[
\begin{gather}
B=\rho gb^{3} \tag{VIII}
\end{gather}
\]
Substituting expressions (III) and (VI), to block B, into expression (V)
\[
\begin{gather}
m_{B}g-T-\rho gb^{3}=m_{B}a \tag{IX}
\end{gather}
\]
Expressions (IV) and (IX) can be written as a system of two equations to two unknowns, a and T
\[
\left\{
\begin{array}{l}
T-m_{A}g=m_{A}a\\
m_{B}g-T-\rho gb^{3}=m_{B}a
\end{array}
\right.
\]
substituting the values given in the problem and adding the two equations
\[
\begin{gather}
\left\{
\begin{array}{l}
T-100\times 10=100a\\
300\times 10-T-1000\times 10\times (0.60)^{3}=300a
\end{array}
\right. \\[10pt]
\left\{
\begin{array}{l}
T-1000=100a\\
3000-T-10000\times 0.216=300a
\end{array}
\right. \\[10pt]
\left\{
\begin{array}{l}
T-1000=100a\\
3000-T-10000\times 0.216=300a
\end{array}
\right. \\[10pt]
\left\{
\begin{array}{l}
T-1000=100a\\
3000-T-2160=300a
\end{array}
\right. \\[10pt]
\frac{
\begin{aligned}
\cancel{T}-1000=100a\\
\text{(+)}\qquad 840-\cancel{T}=300a
\end{aligned}
}
{-160=400a}\\
a=-\frac{160}{400}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{a=-0.4\;\text{m/s}^{2}}
\]
Note: The negative sign indicates that the system moves in the opposite direction to what was
chosen, block A descends and block B rises. This is because, on block B acts the
buoyant force (B), which decreases the effect of the gravitational force on block B.
This result is only valid as block B is immersed in the water, moving with constant acceleration.
As the buoyant force is proportional to the volume of liquid displaced by the body, the expression (IV), the instant the body begins to leave the water, the buoyant force decrease (Figure 4), and the acceleration is no longer constant.
 Figure 4
Figure 4
This result is only valid as block B is immersed in the water, moving with constant acceleration.
As the buoyant force is proportional to the volume of liquid displaced by the body, the expression (IV), the instant the body begins to leave the water, the buoyant force decrease (Figure 4), and the acceleration is no longer constant.

b) Substituting the value found in item (a) in the first, or the second equation of the system, we have the tension force on the rope
\[
\begin{gather}
T-1000=100\times (-0.4)\\
T-1000=-40\\
T=1000-40
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{T=960\;\text{N}}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .