Solved Problem on Mesh Analysis
advertisement
In the circuit below find the currents in the branches and their directions.
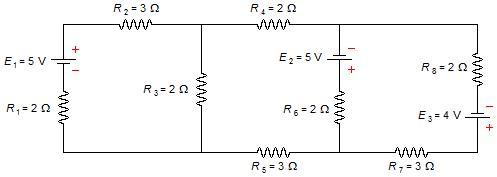
Problem Data:
Resistors:
- R1 = 2 Ω;
- R2 = 3 Ω;
- R3 = 2 Ω;
- R4 = 2 Ω;
- R5 = 3 Ω;
- R6 = 2 Ω;
- R7 = 3 Ω;
- R8 = 2 Ω;
- E1 = 5 V;
- E2 = 5 V;
- E3 = 4 V;
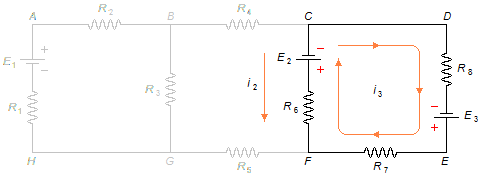
First, to each loop of the circuit is randomly assigned a direction of the current. The meshes ABGHA, BCFGB and CDEFC have, respectively, clockwise currents i1, i2 and i3 (Figure 1)
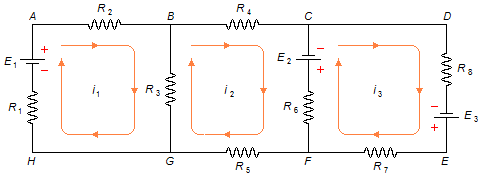
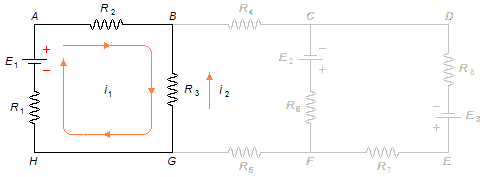
Applying Kirchhoff's Second Law to mesh i1 from point A in the chosen direction, forgetting meshes i2 and i3 (Figure 2)
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\sum_{n} V_{n}=0}
\end{gather}
\]
\[
\begin{gather}
R_{2}i_{1}+R_{3}(i_{1}-i_{2})+R_{1}i_{1}-E_{1}=0
\end{gather}
\]
substituting the problem values
\[
\begin{gather}
3 i_{1}+2(i_{1}-i_{2})+2 i_{1}-5=0\\[5pt]
3 i_{1}+2 i_{1}-2 i_{2}+2 i_{1}=5 \\[5pt]
7 i_{1}-2 i_{2}=5 \tag{I}
\end{gather}
\]
Applying Kirchhoff's Second law to mesh i2 from point B in the chosen
direction, forgetting meshes i1 and i3 (Figure 3)
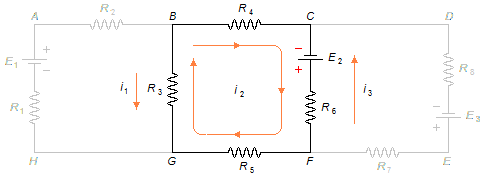
\[
\begin{gather}
R_{4}i_{2}-E_{2}+R_{6}(i_{2}-i_{3})+R_{5}i_{2}+R_{3}(i_{2}-i_{1})=0
\end{gather}
\]
substituting the values
\[
\begin{gather}
2 i_{2}-5+2(i_{2}-i_{3})+3 i_{2}+2(i_{2}-i_{1})=0\\[5pt]
2 i_{2}+2 i_{2}-2 i_{3}+3 i_{2}+2 i_{2}-2 i_{1}=5\\[5pt]
-2 i_{1}+9 i_{2}-2 i_{3}=5 \tag{II}
\end{gather}
\]
Applying Kirchhoff's Second Law to mesh i3 from point C in the chosen
direction, forgetting meshes i1 and i2 (Figure 4)
\[
\begin{gather}
R_{8}i_{3}-E_{3}+R_{7}i_{3}+R_{6}(i_{3}-I_{2})+E_{2}=0
\end{gather}
\]
substituting the values
\[
\begin{gather}
2 i_{3}-4+3 i_{3}+2(i_{3}-i_{2})+5=0\\[5pt]
2 i_{3}+3 i_{3}+2 i_{3}-2 i_{2}+1=0\\[5pt]
-2 i_{2}+7 i_{3}=-1 \tag{III}
\end{gather}
\]
With equations (I), (II) and (III) we have a linear system of three equations with three unknowns
( i1, i2 and i3).
\[
\left\{
\begin{array}{l}
\;\;\,7 i_{1}-2 i_{2}=5\\
-2 i_{1}+9 i_{2}-2 i_{3}=5\\
-2 i_{2}+7 i_{3}=-1
\end{array}
\right. \tag{IV}
\]
solving the first equation for i1, and solving the third equation for i3
\[
\begin{gather}
7 i_{1}-2 i_{2}=5\\[5pt]
7 i_{1}=5+2 i_{2}\\[5pt]
i_{1}=\frac{5+2 i_{2}}{7} \tag{V-a}
\end{gather}
\]
\[
\begin{gather}
-2 i_{2}+7 i_{3}=-1\\[5pt]
7 i_{3}=-1-2 i_{2}\\[5pt]
i_{3}=\frac{-1+2 i_{2}}{7} \tag{V-b}
\end{gather}
\]
substituting the expressions (V-a) and (V-b) in the second equation of system (IV)
\[
\begin{gather}
-2\times \left(\frac{5+2 i_{2}}{7}\right)+9 i_{2}-2\times \left(\frac{-1+2 i_{2}}{7}\right)=5\\[5pt]
\frac{-10-4 i_{2}}{7}+9 i_{2}+\frac{2-4 i_{2}}{7}=5
\end{gather}
\]
multiplying the numerator and denominator of the second term on the left-hac side and the right-hand side
of the equation by 7
\[
\begin{gather}
\frac{-10-4i_{2}}{7}+\frac{7}{7} \times 9i_{2}+\frac{2-4i_{2}}{7}=5 \times \frac{7}{7}\\[5pt]
\frac{-10-4i_{2}}{7}+\frac{63}{7}i_{2}+\frac{2-4i_{2}}{7}=\frac{35}{7}\\[5pt]
\frac{-10-4i_{2}+63i_{2}+2-4i_{2}}{\cancel{7}}=\frac{35}{\cancel{7}}
\end{gather}
\]
canceling factor 7 on both sides of the equation
\[
\begin{gather}
-10-4i_{2}+63i_{2}+2-4i_{2}=35\\[5pt]
-8+55i_{2}=35\\[5pt]
55i_{2}=35+8\\[5pt]
i_{2}=\frac{43}{55}\\[5pt]
i_{2}=0.78\ \text{A}
\end{gather}
\]
Substituting this result in the expressions given in (V-a) and (V-b) we have the currents
i1 and i3
Note: Instead of substituting the current in the decimal form, we will substitute the by
the fraction to minimize rounding errors.
for the expression (V-a) we have the current i1
\[
\begin{gather}
i_{1}=\frac{5+2 \times \dfrac{43}{55}}{7}\\[5pt]
i_{1}=\left(5+2 \times \frac{43}{55}\;\right) \times \frac{1}{7}
\end{gather}
\]
multiplying the numerator and denominator of the first term in parentheses by 55
\[
\begin{gather}
i_{1}=\left(5 \times \frac{55}{55}+2 \times \frac{43}{55}\;\right) \times \frac{1}{7}\\[5pt]
i_{1}=\left(\frac{275}{55}+\frac{86}{55}\;\right) \times \frac{1}{7}\\[5pt]
i_{1}=\frac{361}{55} \times \frac{1}{7}\\[5pt]
i_{1}=\frac{361}{385}\\[5pt]
i_{1}=0,94\ \text{A}
\end{gather}
\]
for the expression (V-b) we have the current i3
\[
\begin{gather}
i_{3}=\frac{-1+2 \times \dfrac{43}{55}}{7}\\[5pt]
i_{3}=\left(-1+2 \times \frac{43}{55}\right) \times \frac{1}{7}
\end{gather}
\]
multiplying the numerator and denominator of the first term in parentheses by 55
\[
\begin{gather}
i_{3}=\left(-1 \times \frac{55}{55}+2 \times \frac{43}{55}\;\right) \times \frac{1}{7}\\[5pt]
i_{3}=\left(\frac{-{55}}{55}+\frac{86}{55}\;\right) \times \frac{1}{7}\\[5pt]
i_{3}=\frac{31}{55} \times \frac{1}{7}\\[5pt]
i_{3}=\frac{31}{385}\\[5pt]
i_{3}=0.08\ \text{A}
\end{gather}
\]
In the branch BG, we have the current i4 given by
\[
\begin{gather}
i_{4}=i_{1}-i_{2}\\[5pt]
i_{4}=\frac{361}{385}-\frac{43}{55}
\end{gather}
\]
multiplying the numerator and denominator of the second term on the right-hand side of the expression by 7
\[
\begin{gather}
i_{4}=\frac{361}{385}-\frac{43}{55}\times\frac{7}{7}\\[5pt]
i_{4}=\frac{361}{385}-\frac{301}{385}\\[5pt]
i_{4}=\frac{361-301}{385}\\[5pt]
i_{4}=\frac{60}{385}
\end{gather}
\]
dividing the numerator and denominator by 5
\[
\begin{gather}
i_{4}=\frac{60:5}{385:5}\\[5pt]
i_{4}=\frac{12}{77}\\[5pt]
i_{4}=0.16\ \text{A}
\end{gather}
\]
The direction of the current i4 will be the same as the current i1
(highest value).In the CF branch, we have the current i5 given by
\[
\begin{gather}
i_{5}=i_{2}-i_{3}\\[5pt]
i_{5}=\frac{43}{55}-\frac{31}{385}
\end{gather}
\]
multiplying the numerator and denominator of the first term on the right-hand side of the expression by 7
\[
\begin{gather}
i_{5}=\frac{43}{55}\times\frac{7}{7}-\frac{31}{385}\\[5pt]
i_{5}=\frac{301}{385}-\frac{31}{385}\\[5pt]
i_{5}=\frac{301-31}{385}\\[5pt]
i_{5}=\frac{270}{385}
\end{gather}
\]
dividing the numerator and denominator by 5
\[
\begin{gather}
i_{5}=\frac{270:5}{385:5}\\[5pt]
i_{5}=\frac{54}{77}\\[5pt]
i_{5}=0.70\ \text{A}
\end{gather}
\]
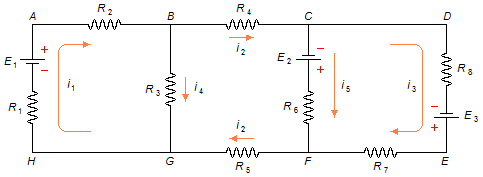
The direction of the current i5 will be the same as the current i2
(highest value).
The currents values are i1=0.99 A, i2=0.78 A, i3=0.08 A, i4=0.16 A, and i5=0.70 A, and their directions are shown in the Figure 5.
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .