Solved Problem on Coulomb's Law

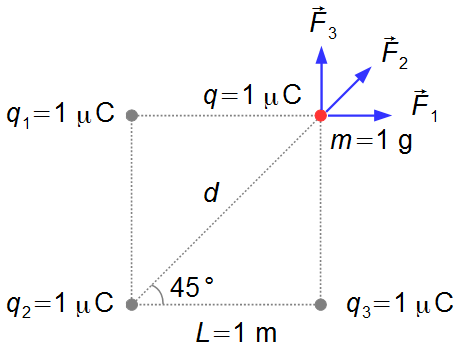
Three electric charges, of 1 μC each, are fixed at the vertices of a square of side 1 m, a particle with a charge of 1 μC and mass 1 g is left at rest at the fourth vertex of the square, at this moment begins to act a repulsive force of the other charges. Determine the acceleration of the particle at the moment it is released.

Problem data:

Value of charges: q = 1 μC;
Free charge mass: m = 1 g;
Distance between charges: L = 1 m;
Coulomb constant \( k_{0}=9\times 10^{9}\;\frac{\mathrm{N.m}^{2}}{\mathrm{C}^{2}} \).

Problem diagram:

The electric force between two charges is in the direction of the line joining these charges, so \( {\vec{F}}_{1} \) is the electric force between charge q and charge q₁, \( {\vec{F}}_{2} \) is the electric force between charge q and charge q₂ and \( {\vec{F}}_{3} \) is the electric force between charge q and charge q₃ (Figure 1).
The distance between charges q and q₂ will be the diagonal d of the square, using the Pythagorean Theorem

\[ \begin{gather} d^{2}=L^{2}+L^{2}\\[5pt] d^{2}=1^{2}+1^{2}\\[5pt] d^{2}=2\\[5pt] d=\sqrt{2\;}\;\mathrm{m} \end{gather} \]

Figure 1

Solution

First, we convert the unit of mass given in grams to kilograms used in the International System of Units (SI).

\[ \begin{gather} m=1\;\cancel{\mathrm{g}}\times\frac{1\;\mathrm{kg}}{1000\;\cancel{\mathrm{g}}}=\frac{1\;\mathrm{kg}}{10^{3}} =1\times10^{-3}\;\mathrm{kg} \end{gather} \]

According to Coulomb's Law, the electric force is given, in magnitude, by

\[ \begin{gather} \bbox[#99CCFF,10px] {F_{E}=k_{0}\frac{|Q_{1}||Q_{2}|}{r^{2}}} \tag{I} \end{gather} \]

We plot the forces on a Cartesian coordinate system instead of taking their components along the x and y directions. Let us plot forces \( {\vec{F}}_{1} \) and \( {\vec{F}}_{3} \) in the direction of \( {\vec{F}}_{2} \) (Figure 2), obtaining the vectors \( {\vec{F}}_{1P} \) and \( {\vec{F}}_{3P} \), which are coincident (this is only possible due to the symmetry of the problem, as all charges are equal, the resultant will be in the direction of \( {\vec{F}}_{2} \)).

Figure 2

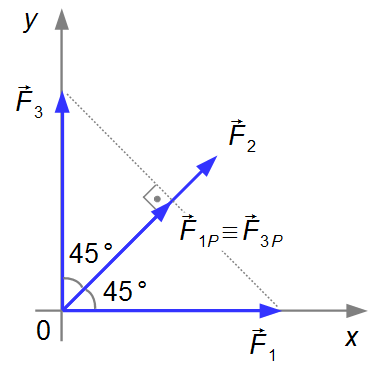
In Figure 2, \( {\vec{F}}_{1} \) is the hypotenuse of the triangle, and \( {\vec{F}}_{1P} \) is a leg, relative to the 45º angle, we can write \( {\vec{F}}_{1P} \).

From the Trigonometry \( \cos 45°=\dfrac{\sqrt{2\;}}{2} \)

\[ \begin{gather} \cos 45°=\frac{\text{adjacent side}}{\mathrm{hypotenuse}}=\frac{F_{1P}}{F_{1}}\\[5pt] F_{1P}=F_{1}\cos 45°\\[5pt] F_{1P}=k_{0}\frac{q\;q_{1}}{L^{2}}\cos 45°\\[5pt] F_{1P}=9\times 10^{9}\times \frac{1\times 10^{-6}\times 1\times 10^{-6}}{{1}^{2}}\times\frac{\sqrt{2\;}}{2}\\[5pt] F_{1P}=9\times 10^{9}\times 1\times 10^{-12}\times\frac{\sqrt{2\;}}{2}\\[5pt] F_{1P}=9\times 10^{-3}\times\frac{\sqrt{2\;}}{2} \tag{II} \end{gather} \]

Analogously we have for \( {\vec{F}}_{3P} \)

\[ \begin{gather} \cos 45°=\frac{\text{adjacent side}}{\mathrm{hypotenuse}}=\frac{F_{3P}}{F_{3}}\\[5pt] F_{3P}=F_{3}\cos 45°\\[5pt] F_{3P}=k_{0}\frac{q\;q_{1}}{L^{2}}\cos 45°\\[5pt] F_{3P}=9\times 10^{9}\times \frac{1\times 10^{-6}\times 1\times 10^{-6}}{{1}^{2}}\times\frac{\sqrt{2\;}}{2}\\[5pt] F_{3P}=9\times 10^{9}\times 1\times 10^{-12}\times\frac{\sqrt{2\;}}{2}\\[5pt] F_{3P}=9\times 10^{-3}\times\frac{\sqrt{2\;}}{2} \tag{III} \end{gather} \]

The magnitude of the force F₂ will be

\[ \begin{gather} F_{2}=k_{0}\frac{q\;q_{2}}{d^{2}}\\[5pt] F_{2}=9\times 10^{9}\times \frac{1\times 10^{-6}\times 1\times 10^{-6}}{\left(\sqrt{2\;}\right)^{2}}\\[5pt] F_{2}=9\times 10^{9}\times 1\times 10^{-12}\times\frac{1}{2}\\[5pt] F_{2}=\frac{9\times 10^{-3}}{2} \tag{IV} \end{gather} \]

The magnitude of the resultant electric force F_E will be the sum of expressions (II), (III), and (IV)

\[ \begin{gather} F_{E}=F_{1P}+F_{3P}+F_{2}\\[5pt] F_{E}=9\times 10^{-3}\times\frac{\sqrt{2\;}}{2}+9\times 10^{-3}\times\frac{\sqrt{2\;}}{2}+\frac{9\times 10^{-3}}{2}\\[5pt] F_{E}=9\times 10^{-3}\times\left(\sqrt{2\;}+\sqrt{2\;}+1\right)\\[5pt] F_{E}=9\times 10^{-3}\times\left(2\sqrt{2\;}+1\right)\\[5pt] F_{E}=1.72\times 10^{-2}\;\mathrm{N} \end{gather} \]

Using Newton's Second Law

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec{F}=m\vec{a}} \end{gather} \]

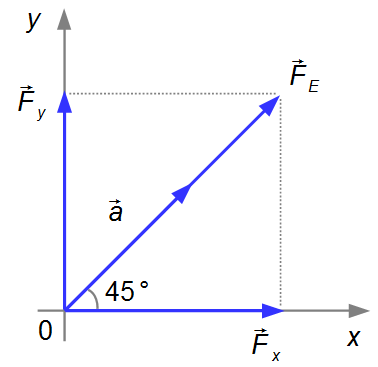
the only force acting on the charge is the electric force F_E, so the acceleration will be in the same direction as the resultant electric force

Figure 3

\[ \begin{gather} F_{E}=ma\\[5pt] a=\frac{F_{E}}{m}\\[5pt] a=\frac{1.72\times 10^{-2}}{1\times 10^{-3}}\\[5pt] a=1.72\times 10^{-2}\times 10^{3}\\[5pt] a=1.72\times 10 \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {a=17.2\;\mathrm{m/s}^{2}} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .