Solved Problem on Capacitors

Twelve capacitors with a capacitance equal to C are used to build the edges of a cube, as shown in the figure. Determine the equivalent capacitance between points A and G that is the diagonal of the cube.

Solution

We assume that capacitors are already charged, neglecting the transient during the time of charge of the capacitors.

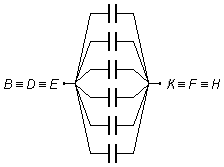
Point A is a circuit node, the potential differences between points A and B, A and D, A and E are the same, therefore points B, D, and E represent the same point in the circuit, \( B\equiv D\equiv E \). The three capacitors "come out" from common point A and "arrive" in the common point \( B\equiv D\equiv E \), so these three capacitors are in parallel (Figure 1).

Figure 1

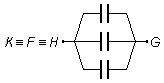
The three capacitors between points K and G, F and G, H and G are also with the same potential differences, points K, F, and H represent the same point in the circuit \( K\equiv F\equiv H \). The capacitors "leave" from the common point \( K\equiv F\equiv H \) and "arrive" in the common point G. These are also in parallel (Figure 2).

Figure 2

The other capacitors are all placed between the common points \( B\equiv D\equiv E \) and \( K\equiv F\equiv H \), they are all in parallel (Figure 3).

Figure 3

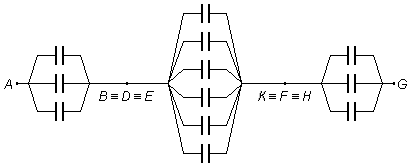
The cube circuit is equivalent to a flat circuit. There are three capacitors in parallel, in series with six capacitors in parallel and in series with three more capacitors in parallel (Figure 4).

Figure 4

Let's call C₁ the equivalent capacitance between points A and \( B\equiv D\equiv E \), and C₃ the equivalent capacitance between points \( K\equiv F\equiv H \) and G, these parts of the circuit are equal, so C₁ = C₃. The expression to determine the equivalent capacitance of an association of n equal capacitors in parallel is

\[ \begin{gather} \bbox[#99CCFF,10px] {C_{eq}=nC} \end{gather} \]

for n = 3

\[ \begin{gather} C_1=C_3=3C \end{gather} \]

Note: we could also determine the equivalent capacitance by applying the expression for the association of capacitors in parallel

\[ \begin{gather} C_{eq}=\sum_{i=1}^{n}C_{i}\\[5pt] C_1=C_3=C+C+C\\[5pt] C_1=C_3=3C \end{gather} \]

Between the points \( B\equiv D\equiv E \) and \( K\equiv F\equiv H \) we have six equal capacitors in parallel we will call the equivalent capacitance between these points C₂, applying the expression to the association in parallel of capacitors, with n = 6, we have

\[ \begin{gather} C_2=6C \end{gather} \]

Note: applying the expression for the association of capacitors in parallel

\[ \begin{gather} C_2=C+C+C+C+C+C\\[5pt] C_2=6C \end{gather} \]

So the circuit is reduced to the following

Figure 5

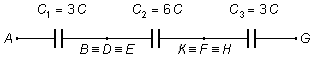
The equivalent capacitance of the circuit C_eq will be the sum of the capacitors in series

\[ \begin{gather} \bbox[#99CCFF,10px] {\frac{1}{C_{eq}}=\sum _{i=1}^{n}{\frac{1}{C_i}}} \end{gather} \]

\[ \begin{gather} \frac{1}{C_{eq}}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}\\[5pt] \frac{1}{C_{eq}}=\frac{1}{3C}+\frac{1}{6C}+\frac{1}{3C} \end{gather} \]

the common factor between 3C and 6C is 6C

\[ \begin{gather} \frac{1}{C_{eq}}=\frac{2+1+2}{6C}\\[5pt] \frac{1}{C_{eq}}=\frac{5}{6C} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {C_{eq}=\frac{6C}{5}} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .