Solved Problem on Prisms
advertisement   



A prism has an apex angle of 60° and an index of refraction of \( \sqrt{2} \). A ray of light focuses on a face with an incidence angle of 45.° Determine:
a) The angle that the ray of light makes with normal when it emerges out of the prism;
b) The angle of total deviation of the ray of light.


Problem data:
  • Apex angle:    Â = 60°;
  • Angle of incidence of the light ray:    î1 = 45°;
  • Index of refraction of the prism:    \( n_{2}=\sqrt{2} \).
Problem diagram:

Assuming that the prism is in the air, the index of refraction of air is 1 (n1 = 1).

Figure 1

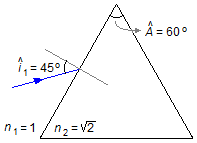
The quantities with index 1 refer to the outside of the prism, and the quantities with index 2 refer to the interior of the prism.

Solution

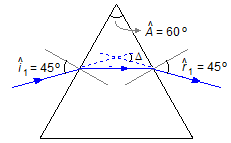
a) The ray of light is refracted into the prism. To find the angle \( \hat{r}_{1} \) that it makes with the normal at the face of the prism, we apply Snell's law (Figure 2).
\[ \bbox[#99CCFF,10px] {n_{1}\operatorname{sen}\theta_{1}=n_{2}\operatorname{sen}\theta _{2}} \]
\[ \begin{gather} n_{1}\operatorname{sen}{\hat{i}}_{1}=n_{2}\operatorname{sen}{\hat{r}}_{2}\\ 1\times \operatorname{sen}45°=\sqrt{2}\operatorname{sen}{\hat{r}}_{2}\\ 1\times \frac{\sqrt{2}}{2}=\sqrt{2}\operatorname{sen}{\hat{r}}_{2}\\ \operatorname{sen}{\hat{r}}_{2}=\frac{1}{\sqrt{2}}\times \frac{\sqrt{2}}{2}\\ \operatorname{sen}{\hat{r}}_{2}=\frac{1}{2}\\ {\hat{r}}_{2}=\operatorname{arc sen}\left(\frac{1}{2}\right)\\ {\hat{r}}_{2}=30° \end{gather} \]
Figure 2

Using the expression between the apex angle Â, the angle of refraction on the first face \( {\hat{r}}_{2} \) and the angle of incidence on the second face \( {\hat{i}}_{2} \) (Figure 3), we have
\[ \bbox[#99CCFF,10px] {\hat{A}={\hat{r}}_{2}+{\hat{i}}_{2}} \]
\[ \begin{gather} 60°=30°+{\hat{i}}_{2}\\ {\hat{i}}_{2}=60°-30°\\ {\hat{i}}_{2}=30° \end{gather} \]
Figure 3

The ray of light is refracted on the second face out of the prism. To find the angle \( {\hat{r}}_{1} \) that it makes with the normal at the face of the prism, we applied, again, the law of Snell's law (Figure 4)

\[ \begin{gather} n_{2}\operatorname{sen}{\hat{i}}_{2}=n_{1}\operatorname{sen}{\hat{r}}_{1}\\ \sqrt{2}\times \operatorname{sen}30°=1\times \operatorname{sen}{\hat{r}}_{1}\\ \sqrt{2}\times \frac{1}{2}=\operatorname{sen}{\hat{r}}_{1}\\ \operatorname{sen}{\hat{r}}_{1}=\frac{\sqrt{2}}{2}\\ {\hat{r}}_{1}=\operatorname{arc sen}\left(\frac{\sqrt{2}}{2}\right) \end{gather} \]
\[ \bbox[#FFCCCC,10px] {{\hat{r}}_{1}=45°} \]
Figure 4

b) The total angle of deviation is given by (Figure 5)
\[ \bbox[#99CCFF,10px] {\Delta={\hat{i}}_{1}+{\hat{r}}_{1}-\hat{A}} \]
\[ \Delta =45°+45°-60° \]
\[ \bbox[#FFCCCC,10px] {\Delta =30°} \]
Figure 5
advertisement   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .