Exercício Resolvido de Trabalho e Energia

Um corpo se move em uma trajetória retilínea, o gráfico da força que atua no corpo em função da distância percorrida é apresentado na figura a seguir.

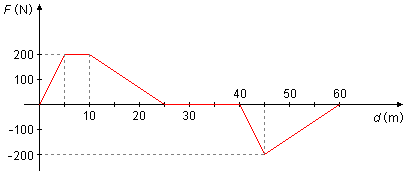
a) Entre que pontos da trajetória não há força atuando sobre o corpo, entre quais pontos a força é motora e entre quais pontos é resistente?
b) Qual é o trabalho da força entre os pontos 0 e 60 m?

Solução:

a) Entre os pontos 25 e 40 m a força é nula, F = 0, não há força atuando sobre o corpo.
Entre os pontos 0 e 25 m a força é positiva, F>0, está no mesmo sentido do deslocamento, a força é motora (e.g. a força do motor de um carro).
Entre os pontos 40 e 60 m a força é negativa, F<0, está no sentido contrário do deslocamento, a força é de resistência (e.g. a força exercida pelo freio de um carro).

Observação: e.g. é a abreviação da expressão em latim “exempli gratia” que significa “por exemplo”.

b) O trabalho da força F entre 0 e 25 m será numericamente igual à área do trapézio sob a curva no gráfico e o eixo Ox, destacado em cinza (Figura 1). A área do trapézio é dada por

\[ \begin{gather} \bbox[#99CCFF,10px] {A=\frac{(B+b)h}{2}} \end{gather} \]

Figura 1

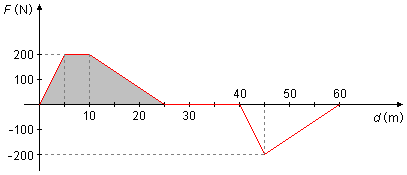
usando os valores do gráfico

\[ \begin{gather} _{\small F}W_{0}^{25}\;\overset{\mathrm N}{=}A=\frac{[25+(10-5)]\times200}{2} \\[5pt] _{\small F}W_{0}^{25}=3000\;\mathrm J \end{gather} \]

Entre os pontos 25 e 40 m a força que atua no corpo é nula, F = 0, o trabalho será nulo.

\[ \begin{gather} _{\small F}W_{25}^{40}=0 \end{gather} \]

Entre os pontos 40 e 60 m o trabalho será numericamente igual à área do triângulo sob o eixo Ox e a curva, em cinza (Figura 2). A área do triângulo é dada por

\[ \begin{gather} \bbox[#99CCFF,10px] {A=\frac{B\;h}{2}} \end{gather} \]

Figura 2

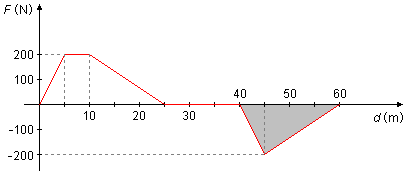
usando os valores do gráfico

\[ \begin{gather} _{\small F}W_{40}^{60}\;\overset{\mathrm N}{=}A=\frac{(60-40)\times(-200)}{2} \\[5pt] _{\small F}W_{40}^{60}=-2000\;\mathrm J \end{gather} \]

O trabalho total da força F será dado pela soma das três partes calculadas acima.

\[ \begin{gather} _{\small F}W_{0}^{60}=_{\small F}W_{0}^{25}+_{\small F}W_{25}^{40}+_{\small F}W_{40}^{60} \\[5pt] _{\small F}W_{0}^{60}=3000+0+(-2000) \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {_{\small F}W_{0}^{60}=1000\;\mathrm J} \end{gather} \]

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .