Solved Problem on Coulomb's Law and Electric Field
advertisement
A semicircular plate has an outer radius of a and an inner radius of b. The plate carries
a total charge Q distributed non uniformly, the charge is directly proportional to the central
angle θ that a semicircle
\( 0 \leq \theta \leq \pi \).
Calculate the electric field vector at a point P on the axis of the semicircle perpendicular to
the plane passing through the center of curvature at a distance z from its center.
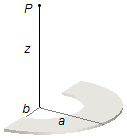
Problem data:
- External radius of the semicircle: a;
- Inner radius of the semicircle: b;
- Charge of the plate: Q;
- Distance to the point where we want the electric field: z.
The surface density of charge of the plate is directly proportional to the angular position of the
charge (Figure 1)
\[
\begin{gather}
\sigma (\theta )=\alpha \;\theta \tag{I}
\end{gather}
\]
where α is a constant that makes the expression dimensionally consistent.

Figure 1
The position vector r goes from an element of charge dq to point P where we want to calculate the electric field, the vector rq locates the charge element relative to the origin of the reference frame, and the vector rp locates point P (Figure 2-A).
\[
\mathbf{r}={\mathbf{r}}_{p}-{\mathbf{r}}_{q}
\]

Based on the geometry of the problem, we choose cylindrical coordinates (Figure 2-B), the vector rq only has a component in the er direction, \( {\mathbf{r}}_{q}=r_{q}\;\mathbf{e}_{r} \) and the vector rp only has a component in the z direction, \( {\mathbf{r}}_{p}=r_{p}\;\mathbf{e}_{z} \). Converting cylindrical coordinates to Cartesian coordinates x, y and z are given by
\[
\left\{
\begin{array}{l}
x=r_{q}\cos \theta \\
y=r_{q}\operatorname{sen}\theta \\
z=z
\end{array}
\right. \tag{II}
\]
Note: In the Figure 2-B, i, j e k are unit vectors in the Cartesian
coordinates, and er, eθ e
ez are unit vectors in the cylindrical coordinates.
After the conversion the vector rq, is written as \( {\mathbf{r}}_{q}=x\;\mathbf{i}+y\;\mathbf{j} \), and the vector rp as \( {\mathbf{r}}_{p}=z\;\mathbf{k} \).
The position vector will be
\[
\begin{gather}
\mathbf{r}=z\;\mathbf{k}-\left(x\;\mathbf{i}+y\;\mathbf{j}\right)\\
\mathbf{r}=-x\;\mathbf{i}-y\;\mathbf{j}+z\;\mathbf{k} \tag{III}
\end{gather}
\]
From expression (III), the magnitude of the position vector r will be
\[
\begin{gather}
r^{2}=(-x)^{2}+(-y)^{2}+z^{2}\\
r=\left(x^{2}+y^{2}+z^{2}\right)^{\frac{1}{2}} \tag{IV}
\end{gather}
\]
Solution
The electric field vector is given by
\[ \bbox[#99CCFF,10px]
{\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\int{\frac{dq}{r^{2}}\;\frac{\mathbf{r}}{r}}}
\]
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\int{\frac{dq}{r^{3}}\;\mathbf{r}} \tag{V}
\end{gather}
\]
Using the expression of the surface density of charge σ, we have the charge element dq
\[ \bbox[#99CCFF,10px]
{\sigma =\frac{dq}{dA}}
\]
\[
\begin{gather}
dq=\sigma(\theta) \;dA \tag{VI}
\end{gather}
\]
where dA is an element of area.The area element in Cartesian coordinates is
\[
dA=dx \;dy
\]
to obtain the area element in polar coordinates, we calculate the Jacobian given by the determinant
\[
J=\left|
\begin{matrix}
\;\dfrac{\partial x}{\partial r}&\dfrac{\partial
x}{\partial \theta }\;\\
\;\dfrac{\partial y}{\partial r}&\dfrac{\partial
y}{\partial \theta }\;
\end{matrix}
\right|
\]
Calculation of partial derivatives of x and y functions given by expressions in (II)
\( x=r_{q}\cos \theta \):
\( \dfrac{\partial x}{\partial r_{q}}=\dfrac{\partial (r_{q}\cos \theta)}{\partial r_{q}}=\cos \theta \dfrac{\partial r_{q}}{\partial r_{q}}=\cos \theta .1=\cos \theta \text{, } \)
\( \dfrac{\partial x}{\partial \theta }=\dfrac{\partial (r_{q}\cos \theta)}{\partial \theta }=r_{q}\dfrac{\partial (\cos \theta )}{\partial\theta }=r_{q}(-\sin \theta)=-r_{q}\sin \theta \text{, } \)
\( y=r_{q}\sin \theta \):
\( \dfrac{\partial y}{\partial r_{q}}=\dfrac{\partial(r_{q}\sin \theta )}{\partial r_{q}}=\sin \theta \dfrac{\partial r_{q}}{\partial r_{q}}=\sin \theta .1=\sin \theta \text{, } \)
\( \dfrac{\partial y}{\partial \theta }=\dfrac{\partial(r_{q}\sin \theta )}{\partial \theta }=r_{q}\dfrac{\partial(\sin \theta )}{\partial \theta }=r_{q}\cos \theta \text{, } \)
\( x=r_{q}\cos \theta \):
\( \dfrac{\partial x}{\partial r_{q}}=\dfrac{\partial (r_{q}\cos \theta)}{\partial r_{q}}=\cos \theta \dfrac{\partial r_{q}}{\partial r_{q}}=\cos \theta .1=\cos \theta \text{, } \)
\[ \dfrac{\partial x}{\partial r_{q}}=\dfrac{\partial (r_{q}\cos \theta)}{\partial r_{q}}=\cos \theta \dfrac{\partial r_{q}}{\partial r_{q}}=\cos \theta .1=\cos \theta \]
in the derivative in rq, the value of θ is constant, and the cosine is moved
outside of the derivative.
\( \dfrac{\partial x}{\partial \theta }=\dfrac{\partial (r_{q}\cos \theta)}{\partial \theta }=r_{q}\dfrac{\partial (\cos \theta )}{\partial\theta }=r_{q}(-\sin \theta)=-r_{q}\sin \theta \text{, } \)
\[ \dfrac{\partial x}{\partial \theta }=\dfrac{\partial (r_{q}\cos \theta)}{\partial \theta }=r_{q}\dfrac{\partial (\cos \theta )}{\partial\theta }=r_{q}(-\sin \theta)=-r_{q}\sin \theta \]
in the derivative in θ, the value of rq is constant, and it is moved outside of
the derivative.
\( y=r_{q}\sin \theta \):
\( \dfrac{\partial y}{\partial r_{q}}=\dfrac{\partial(r_{q}\sin \theta )}{\partial r_{q}}=\sin \theta \dfrac{\partial r_{q}}{\partial r_{q}}=\sin \theta .1=\sin \theta \text{, } \)
\[ \dfrac{\partial y}{\partial r_{q}}=\dfrac{\partial(r_{q}\sin \theta )}{\partial r_{q}}=\sin \theta \dfrac{\partial r_{q}}{\partial r_{q}}=\sin \theta .1=\sin \theta \]
in the derivative in rq, the value of θ is constant, and the sine is moved
outside of the derivative.
\( \dfrac{\partial y}{\partial \theta }=\dfrac{\partial(r_{q}\sin \theta )}{\partial \theta }=r_{q}\dfrac{\partial(\sin \theta )}{\partial \theta }=r_{q}\cos \theta \text{, } \)
\[ \dfrac{\partial y}{\partial \theta }=\dfrac{\partial(r_{q}\sin \theta )}{\partial \theta }=r_{q}\dfrac{\partial(\sin \theta )}{\partial \theta }=r_{q}\cos \theta \]
in the derivative in θ, the value of rq is constant, and it is moved outside of
the derivative.
\[
dA=dx\;dy=J\;dr_{q}\;d\theta
\]
\[
\begin{gather}
J=\left|
\begin{matrix}
\;\cos \theta & -r_{q}\sin \theta \;\\
\;\sin \theta & r_{q}\cos \theta
\end{matrix}\right|\\[5pt]
J=\cos \theta .r_{q}\cos \theta-(-r_{q}\sin \theta .\sin \theta)\\[5pt]
J=r_{q}\cos ^{2}\theta +r_{q}\sin ^{2}\theta\\[5pt]
J=r_{q}(\underbrace{\cos ^{2}\theta +\sin ^{\;2}\theta}_{1})\\[5pt]
J=r_{q}
\end{gather}
\]
\[
\begin{gather}
dA=r_{q}\;dr_{q}\;d\theta \tag{VII}
\end{gather}
\]
substituting the expressions (I) and (VII) into expression (VI)
\[
\begin{gather}
dq=\alpha \theta r_{q}\;dr_{q}\;d\theta \tag{VIII}
\end{gather}
\]
Substituting expressions (III), (IV), and (VI) into expression (V), and as the integration is made on the
surface of the plate, it depends on two variables rq and θ, we have a double integral
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\iint{\frac{\alpha \theta r_{q}\;dr_{q}\;d\theta}{\left[\left(x^{2}+y^{2}+z^{2}\right)^{\frac{1}{2}}\right]^{3}}}\left(-x\;\mathbf{i}-y\;\mathbf{j}+z\;\mathbf{k}\right)\\
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\iint{\frac{\alpha \theta r_{q}\;dr_{q}\;d\theta}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}}}\left(-x\;\mathbf{i}-y\;\mathbf{j}+z\;\mathbf{k}\right) \tag{IX}
\end{gather}
\]
substituting the expressions (II) into expression (IX)
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\iint{\frac{\alpha \theta r_{q}\;dr_{q}\;d\theta}{\left[\left(r_{q}\cos \theta\right)^{2}+\left(r_{q}\sin \theta\right)^{2}+z^{2}\right]^{\frac{3}{2}}}\left(-r_{q}\cos \theta\;\mathbf{i}-r_{q}\sin \theta\;\mathbf{j}+z\;\mathbf{k}\right)}\\[5pt]
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\iint{\frac{\alpha \theta r_{q}\;dr_{q}\;d\theta}{\left[r_{q}^{2}\cos ^{2}\theta +r_{q}^{2}\sin ^{2}\theta+z^{2}\right]^{\frac{3}{2}}}\left(-r_{q}\cos \theta\;\mathbf{i}-r_{q}\sin \theta\;\mathbf{j}+z\;\mathbf{k}\right)}\\[5pt]
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\iint{\frac{\alpha \theta r_{q}\;dr_{q}\;d\theta}{\left[r_{q}^{2}\underbrace{\left(\cos ^{2}\theta+\sin ^{2}\theta\right)}_{1}+z^{2}\right]^{\frac{3}{2}}}\left(-r_{q}\cos \theta\;\mathbf{i}-r_{q}\sin \theta\;\mathbf{j}+z\;\mathbf{k}\right)}\\[5pt]
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\iint{\frac{\alpha \theta r_{q}\;dr_{q}\;d\theta}{\left(r_{q}^{2}+z^{2}\right)^{\frac{3}{2}}}\left(-r_{q}\cos \theta\;\mathbf{i}-r_{q}\sin \theta\;\mathbf{j}+z\;\mathbf{k}\right)}
\end{gather}
\]
As α is constant it is moved outside of the integral, and the integral of the sum is equal to the
sum of the integrals
\[
\mathbf{E}=\frac{\alpha}{4\pi \epsilon_{0}}\left(-\iint{\frac{r_{q}^{2}\theta \cos \theta \;dr_{q}\;d\theta}{\left(r_{q}^{2}+z^{2}\right)^{\frac{3}{2}}}}\;\mathbf{i}-\iint{\frac{r_{q}^{2}\theta \sin \theta \;dr_{q}\;d\theta}{\left(r_{q}^{2}+z^{2}\right)^{\frac{3}{2}}}}\;\mathbf{j}+z\iint{\frac{r_{q}\theta \;dr_{q}\;d\theta}{\left(r_{q}^{2}+z^{2}\right)^{\frac{3}{2}}}}\;\mathbf{k}\right)
\]
The limits of integration will be b and a in drq, along the radius of the
semicircular plate, 0 and 2π in dθ, a half-turn, the integral can be separated
\[
\begin{split}
\mathbf{E}=&\frac{\alpha}{4\pi\epsilon_{0}}\left(-\int_{b}^{a}{\frac{r_{q}^{2}\;dr_{q}}{\left(r_{q}^{2}+z^{2}\right)^{\frac{3}{2}}}}\int_{0}^{\pi}\theta \cos \theta \;d\theta\;\mathbf{i}-\int_{b}^{a}{\frac{r_{q}^{2}\;dr_{q}}{\left(r_{q}^{2}+z^{2}\right)^{\frac{3}{2}}}}\int_{0}^{\pi}\theta \operatorname{sen}\theta \;d\theta\;\mathbf{j}+\right.\\
&\left. +z\int_{b}^{a}{\frac{r_{q}\;dr_{q}}{\left(r_{q}^{2}+z^{2}\right)^{\frac{3}{2}}}}\int_{0}^{\pi}\theta \;d\theta \;\mathbf{k}\right)
\end{split}
\]
factoring the term
\( \int_{b}^{a}{\frac{r_{q}^{2}\;dr_{q}}{\left(r_{q}^{2}+z^{2}\right)^{\frac{3}{2}}}} \)
\[
\mathbf{E}=\frac{\alpha}{4\pi \epsilon_{0}}\int_{b}^{a}{\frac{r_{q}^{2}\;dr_{q}}{\left(r_{q}^{2}+z^{2}\right)^{\frac{3}{2}}}}\left(-\int_{0}^{\pi}\theta \cos \theta \;d\theta\;\mathbf{i}-\int _{0}^{\pi}\theta\sin \theta \;d\theta \;\mathbf{j}+z\int_{0}^{\pi}\theta \;d\theta \;\mathbf{k}\right)
\]
Integration of \( \displaystyle \int_{b}^{a}{\frac{r_{q}\;dr_{q}}{\left(r_{q}^{2}+z^{2}\right)^{\frac{3}{2}}}} \)
Changing the variable
for rq = b
we have \( u=b^{2}+z^{2} \)
for rq = a
we have \( u=a^{2}+z^{2} \)
Changing the variable
\[
\begin{array}{l}
u=r_{q}^{2}+z^{2}\\
\dfrac{du}{dr_{q}}=2r_{q}\Rightarrow dr_{q}=\dfrac{du}{2r_{q}}
\end{array}
\]
changing the limits of integration
for rq = b
we have \( u=b^{2}+z^{2} \)
for rq = a
we have \( u=a^{2}+z^{2} \)
\[
\begin{align}
\int_{{b^{2}+z^{2}}}^{{a^{2}+z^{2}}}{\frac{r_{q}}{u^{\frac{3}{2}}}\;\frac{du}{2r_{q}}} &\Rightarrow\frac{1}{2}\int_{{b^{2}+z^{2}}}^{{a^{2}+z^{2}}}{\frac{1}{u^{\frac{3}{2}}}\;du}\Rightarrow\;\frac{1}{2}\left.\frac{u^{-{\frac{3}{2}+1}}}{-{\left(\frac{3}{2}+1\right)}}\;\right|_{\;b^{2}+z^{2}}^{\;a^{2}+z^{2}}\Rightarrow \\[5pt]
&\Rightarrow\frac{1}{2}\left.\frac{u^{\frac{-3+2}{2}}}{\left(\frac{-{3+2}}{2}\right)}\;\right|_{\;b^{2}+z^{2}}^{\;a^{2}+z^{2}}\Rightarrow \cancel{\frac{1}{2}}\left.\frac{u^{-{\frac{1}{2}}}}{-{\cancel{\frac{1}{2}}}}\;\right|_{\;b^{2}+z^{2}}^{\;a^{2}+z^{2}}\Rightarrow \\[5pt]
&\Rightarrow\left.-u^{-{\frac{1}{2}}}\;\right|_{\;b^{2}+z^{2}}^{\;a^{2}+z^{2}}\Rightarrow\left.-{\frac{1}{u^{\frac{1}{2}}}}\;\right|_{\;b^{2}+z^{2}}^{\;a^{2}+z^{2}}\Rightarrow \\[5pt]
&\Rightarrow-\left(\frac{1}{\sqrt{a^{2}+z^{2}}}-\frac{1}{\sqrt{\;b^{2}+z^{2}}}\right)\Rightarrow\\[5pt]
&\Rightarrow\frac{1}{\sqrt{b^{2}+z^{2}\;}}-\frac{1}{\sqrt{\;a^{2}+z^{2}\;}}
\end{align}
\]
Integration of \( \displaystyle \int_{0}^{\pi}\theta \cos \theta \;d\theta \)
Using Integration by Parts \( \int uv'=uv-\int u'v \), we chose
Using Integration by Parts \( \int uv'=uv-\int u'v \), we chose
\[
\begin{array}{l}
u=\theta \qquad \qquad \; v'=\cos \theta \\
u'=1\qquad \qquad v=\sin \theta
\end{array}
\]
\[
\begin{align}
\int_{0}^{\pi}\theta \cos \theta \;d\theta &=\theta\sin \theta |_{\;0}^{\;\pi}-\int_{0}^{\pi}\sin \theta \;d\theta\Rightarrow\\[5pt]
&\Rightarrow\theta \sin \theta \;|_{\;0}^{\;\pi}-\left(-\cos \theta \;|_{\;0}^{\;\pi}\right)\Rightarrow\\[5pt]
&\Rightarrow\theta \sin \theta \;|_{\;0}^{\;\pi}+\cos \theta \;|_{\;0}^{\;\pi}\Rightarrow\\[5pt]
&\Rightarrow\left(\pi.\sin \pi-0.\sin 0\;\right)+\left(\cos \pi -\cos 0\right)\Rightarrow\\[5pt]
&\Rightarrow\left(\pi.0-0.0\right)+\left(-1-1\right)\Rightarrow-2
\end{align}
\]
Integration of \( \displaystyle \int_{0}^{\pi}\theta \sin \theta \;d\theta \)
Using Integration by Parts \( \int uv'=uv-\int u'v \), we chose
Using Integration by Parts \( \int uv'=uv-\int u'v \), we chose
\[
\begin{array}{l}
u=\theta\qquad \qquad \; v'=\sin \theta \\
u'=1\qquad \qquad v=-\cos \theta
\end{array}
\]
\[
\begin{align}
\int_{0}^{\pi}\theta \sin \theta\;d\theta &=-\theta \cos \theta \;|_{\;0}^{\;\pi}-\int_{0}^{\pi}-\cos\theta \;d\theta\Rightarrow\\[5pt]
&\Rightarrow-\theta \cos \theta \;|_{\;0}^{\;\pi}+\int_{0}^{\pi}\cos\theta \;d\theta\Rightarrow\\[5pt]
&\Rightarrow-\theta \cos \theta \;|_{\;0}^{\;\pi}+\sin \theta \;|_{0}^{\pi}\Rightarrow\\[5pt]
&\Rightarrow-\left(\pi .\cos \pi -0.\cos0\right)+\left(\sin \pi -\sin 0\right)\Rightarrow\\[5pt]
&\Rightarrow-\left[\pi.(-1)-0.1\right]+\left(0-0\right)\Rightarrow\\[5pt]
&\Rightarrow\int_{0}^{\pi}\theta \sin \theta\;d\theta \Rightarrow\pi
\end{align}
\]
Integration of \( \displaystyle \int_{0}^{\pi}\;d\theta \)
\[
\int_{0}^{\pi}\;d\theta =\left.\theta \;\right|_{\;0}^{\;\pi}=\pi-0=\pi
\]
\[
\mathbf{E}=\frac{\alpha}{4\pi \epsilon_{0}}\left(\frac{1}{\sqrt{b^{2}+z^{2}}}-\frac{1}{\sqrt{a^{2}+z^{2}\;}}\right)\left[-(-2)\;\mathbf{i}-\pi\;\mathbf{j}+z\pi \;\mathbf{k}\right]
\]
\[ \bbox[#FFCCCC,10px]
{\mathbf{E}=\frac{\alpha}{4\pi \epsilon_{0}}\left(\frac{1}{\sqrt{b^{2}+z^{2}\;}}-\frac{1}{\sqrt{a^{2}+z^{2}\;}}\right)\left(2\;\mathbf{i}-\pi\;\mathbf{j}+z\pi \;\mathbf{k}\right)}
\]

Figure 3
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .