Solved Problem on Linear Momentum
advertisement
Two boats sail parallel to each other with the same speed. When the boats cross, a load from one boat is thrown to the other, and then another equal load is thrown from the second boat to the first. In another case, the loads are released simultaneously. In what case the speed of the boats will be higher after the loads are thrown?
Problem data:
- Mass of boat: M;
- Mass of loads: m;
- Initial speed of boat: v0.
- Case in which one of the loads is launched after the other
We choose a reference frame pointing to the right in the direction of the displacement of the boat (a),
Figure 1.
In the initial situation for boat (a), its mass is the sum of the masses of the boat and the load (M+m) and navigates with velocity v0. The load in the boat (b) has mass m and moves with the boat velocity (−v0), so when this mass is thrown into the boat (a) it transfers to this a momentum equal to −mv0 (Figure 1-A).
In the final situation, boat (a) has mass (M+2m) and velocity v1 (Figure 1-B).
In the initial situation for boat (b), its mass is m, its load has already been thrown to boat (a), and navigates with velocity −v0. The load in the boat (a) has mass m and moves at the same velocity as the boat v1, so when this mass is thrown into the boat (b) it transfers to this a momentum equal to mv1 motion (Figure 1-C).
In the final situation, boat (b) has mass (M+m) and velocity −v2 (Figure 1-D).
In the initial situation for boat (a), its mass is the sum of the masses of the boat and the load (M+m) and navigates with velocity v0. The load in the boat (b) has mass m and moves with the boat velocity (−v0), so when this mass is thrown into the boat (a) it transfers to this a momentum equal to −mv0 (Figure 1-A).
In the final situation, boat (a) has mass (M+2m) and velocity v1 (Figure 1-B).
In the initial situation for boat (b), its mass is m, its load has already been thrown to boat (a), and navigates with velocity −v0. The load in the boat (a) has mass m and moves at the same velocity as the boat v1, so when this mass is thrown into the boat (b) it transfers to this a momentum equal to mv1 motion (Figure 1-C).
In the final situation, boat (b) has mass (M+m) and velocity −v2 (Figure 1-D).

The momentum is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{Q=mv}
\end{gather}
\]
Using the Law of Conservation of Momentum write for each of the boats
- Boat (a)
\[
\begin{gather}
{_{a}Q_{i}}={_{a}Q_{f}}\\[5pt]
(M+m)v_{0}-mv_{0}=(M+2m)v_{1} \tag{I}
\end{gather}
\]
- Boat (b)
\[
\begin{gather}
{_{b}Q_{i}}={_{b}Q_{f}}\\[5pt]
-Mv_{0}+mv_{1}=(M+m)v_{2} \tag{II}
\end{gather}
\]
The expressions (I) and (II) can be written as a system of two equations to two unknowns
(v1 and v2)
\[
\left\{
\begin{array}{l}
\;(M+m)v_{0}-mv_{0}=(M+2m)v_{1}\\[5pt]
\;-Mv_{0}+mv_{1}=(M+m)v_{2}
\end{array}
\right.
\]
from the first equation
\[
\begin{gather}
Mv_{0}+mv_{0}-mv_{0}=(M+2m)v_{1}\\[5pt]
Mv_{0}=(M+2m)v_{1}\\[5pt]
v_{1}=\frac{M}{M+2m}v_{0} \tag{III}
\end{gather}
\]
substituting the expression (III) into the second equation of the system
\[
\begin{gather}
-Mv_{0}+m\frac{M}{M+2m}v_{0}=(M+m)v_{2}
\end{gather}
\]
multiplying both sides of the equation by (M+2m)
\[
\begin{gather}
-(M+2m)Mv_{0}+\cancel{(M+2m)}m\frac{M}{\cancel{M+2m}}v_{0}=(M+2m)(M+m)v_{2}\\[5pt]
-M^{2}v_{0}-2Mmv_{0}+Mmv_{0}=(M+2m)(M+m)v_{2}\\[5pt]
-M^{2}v_{0}-Mmv_{0}=(M+2m)(M+m)v_{2}\\[5pt]
-Mv_{0}\cancel{(M+m)}=(M+2m)\cancel{(M+m)}v_{2}\\[5pt]
-Mv_{0}=(M+2m)v_{2}\\[5pt]
v_{2}=-\frac{{M}}{M+2m}v_{0} \tag{IV}
\end{gather}
\]
With the expressions (III) and (IV) we can write
\[
\begin{gather}
v_{1}=-v_{2}=\frac{M}{M+2m}v_{0} \tag{V}
\end{gather}
\]
- Case in which the loads are released simultaneously
We choose the same reference frame as the previous situation (Figure 2).
In the initial situation for boat (a), its load has already been launched and it transfers a momentum of mv0 to the boat (b), its mass is M, and navigates with velocity v0. Simultaneously boat (b) throws its load and transfers a momentum −mv0 to boat (a), its mass is m and navigates with velocity −v0 (Figure 2-A).
In the final situation, boat (a) has mass (M+m) and velocity v3. In the final situation, boat (b) has mass (M+m) and velocity −v4 (Figure 2-B).
In the initial situation for boat (a), its load has already been launched and it transfers a momentum of mv0 to the boat (b), its mass is M, and navigates with velocity v0. Simultaneously boat (b) throws its load and transfers a momentum −mv0 to boat (a), its mass is m and navigates with velocity −v0 (Figure 2-A).
In the final situation, boat (a) has mass (M+m) and velocity v3. In the final situation, boat (b) has mass (M+m) and velocity −v4 (Figure 2-B).
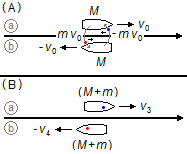
Using the Law of Conservation of Momentum we write for each of the boats
- Boat (a)
\[
\begin{gather}
{_{a}Q_{i}}={_{a}Q_{f}}\\[5pt]
Mv_{0}-mv_{0}=(M+m)v_{3} \tag{VI}
\end{gather}
\]
- Boat (b)
\[
\begin{gather}
{_{b}Q_{i}}={_{b}Q_{f}}\\[5pt]
-Mv_{0}+mv_{0}=(M+m)v_{4} \tag{VII}
\end{gather}
\]
from the expression (VI)
\[
\begin{gather}
(M-m)v_{0}=(M+m)v_{3}\\[5pt]
v_{3}=\frac{M-m}{M+m}v_{0} \tag{VIII}
\end{gather}
\]
from the expression (VII)
\[
\begin{gather}
-(M-m)v_{0}=(M+m)v_{4}\\[5pt]
v_{4}=\frac{-{M-m}}{M+m}v_{0} \tag{IX}
\end{gather}
\]
With the expressions (VIII) and (IX) we can write
\[
\begin{gather}
v_{3}=-v_{4}=\frac{M-m}{M+m}v_{0} \tag{X}
\end{gather}
\]
To find the highest speed we must compare the expressions (V) and (X).To make the expressions in the same denominator we multiply the numerator and the denominator of the expression (V) by (M+m), and the numerator and the denominator of the expression (X) by (M+2m).
\( v_{1}=\dfrac{(M+m)}{(M+m)}.\dfrac{M}{(M+2m)}v_{0}=\dfrac{M^{2}+Mm}{(M+m)(M+2m)}v_{0} \)
\( v_{1}=\dfrac{(M+m)}{(M+m)}.\dfrac{M}{(M+2m)}v_{0}=\dfrac{M^{2}+Mm}{(M+m)(M+2m)}v_{0} \)
\( v_{3}=\dfrac{(M+2m)}{(M+2m)}.\dfrac{(M-m)}{(M+m)}v_{0}=\dfrac{M^{2}-Mm+2Mm-2m^{2}}{(M+m)(M+2m)}v_{0}=\dfrac{M^{2}+Mm-2m^{2}}{(M+m)(M+2m)}v_{0} \)
\( v_{3}=\dfrac{(M+2m)}{(M+2m)}.\dfrac{(M-m)}{(M+m)}v_{0}=\dfrac{M^{2}-Mm+2Mm-2m^{2}}{(M+m)(M+2m)}v_{0}=\dfrac{M^{2}+Mm-2m^{2}}{(M+m)(M+2m)}v_{0} \)
The two expressions above are on the same denominator, in the first expression the numerator is \( M^{2}+Mn \) and in the second expression the numerator this value is subtracted from the value \( 2m^{2} \), so the second fraction represents smaller value
\[
\begin{gather}
v_{1}=\frac{M^{2}+Mm}{(M+m)(M+2m)}v_{0}>\frac{M^{2}+Mm-2m^{2}}{(M+m)(M+2m)}v_{0}=v_{3}\\[5pt]
v_{1}>v_{3}
\end{gather}
\]
The speed in the first case is higher.
Note: When the boat crew acts on the load launching it with a force
\( \vec{F} \),
perpendicular to the trajectory of the boat, it reacts over the boat with a force
\( -\vec{F} \),
this would cause a side displacement of the boat. To avoid this motion, we assume that the mass of
the load is small so that force
\( \vec{F} \)
is such that it can be balanced by the water resistance force
\( {\vec{F}}_{R} \)
acting on the side of the boat (Figure 3).
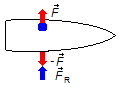
Figure 3
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .